Maandelijks archief: mei 2014

Tegendenken (20): Postmortem (I)

Het wordt een succes
Als je een goed idee hebt is het niet zo moeilijk voor te stellen hoe succesvol dat gaat worden. Neem bijvoorbeeld het plannen van een vakantie. Je bepaalt met wie je weggaat, wanneer je gaat, hoe lang en uiteraard waar naar toe en hoe je gaat overnachten. Hierbij hou je natuurlijk rekening met een aantal factoren zoals bijvoorbeeld het weer. Voor je gevoel heb je een goed plan gemaakt en ben je kritisch geweest. Je bent er dus van overtuigd dat dit een goede vakantie gaat worden. Een paar dagen voordat je de vakantie gaat boeken kom je een vriend tegen die zegt dat je toch een beetje moet tegendenken, om je vakantieplannen robuust te maken. Je probeert wat dingen te bedenken, maar wat je ook bedenkt, het blijft een geweldige vakantie. Gaat het bijvoorbeeld regenen, dan gaan we spelletjes doen en een grot in.

Er is een methode om het tegendenken wat sterker te maken, namelijk het uitgangspunt omdraaien. Bij een vakantie ga je er automatisch vanuit dat het een geslaagde vakantie wordt, alles wat je bedenkt zal daar in passen. Maar als je uitgaat van een mislukte vakantie, dan ziet de wereld er opeens heel anders uit.

Het is mislukt
Leef je eens serieus in, in de volgende situatie:
Je komt terug van vakantie en het is een totaal mislukte vakantie geworden, er was niets aan, de rest van je leven hoef je niet meer op vakantie. (Probeer daar voor jezelf een gevoel bij te krijgen.) Je komt thuis met de auto, een verademing om weer thuis te zijn. Je neemt je voor om morgen meteen met alle vakantiespullen naar de kringloopwinkel te rijden en daar alles achter te laten. Dit nooit weer.

Stel jezelf nu de volgende vragen, “hoe heeft het zo kunnen lopen? Wat hebben we over het hoofd gezien? Wat is er gebeurt?”. Bij mij komt er van alles boven, pech met de auto en een week bezig zijn om dat weer gerepareerd te krijgen, de eerste dag van je fiets vallen en de rest van de vakantie met een gebroken sleutelbeen op een stoel moeten zitten, twee weken met elkaar ruzie maken etc. Niet de leukste gedachten nu de zomer in zicht is. We noemen deze aanpak post-mortem, afgeleid van het onderzoek dat na de dood wordt verricht om de doodsoorzaak te achterhalen.

Met alleen het bedenken van alle problemen ben je er natuurlijk nog niet. Het gaat vervolgens om de vraag wat dit betekent voor de vakantie die je nu aan het plannen bent. Dat kan in dit geval heel simpel zijn door nog eens de reisverzekering door te nemen en te kijken wat die zegt over pech en de verzekering daar op aan te passen. Ook zou ik m’n fiets thuis kunnen laten. Maar misschien zijn complexere maatregelen nodig zoals het kiezen van een ander reisgezelschap. Tja als je de post mortem methode echt goed uitvoert wil je misschien wel nooit meer op vakantie.

Nou is één van de grote verschillen tussen een vakantie en een project dat je op vakantie op zoek bent naar avontuur. Daarom ga je ergens heen waar je de taal misschien niet spreekt, het eten niet lekker vindt en waar ze geen onderdelen hebben voor uitgerekend jouw auto. Maar bij een project, of dat nou klein is (een aanbouw aan je huis) of groot (een hele woonwijk herontwikkelen of een nieuw stadskantoor) gaat het helemaal niet om avontuur en wil je juist op zeker spelen. Dat betekent dat je echt de tijd moet nemen om na te denken over ‘zwarte scenario’s’ en hoe je die of de gevolgen daarvan zoveel mogelijk kunt voorkomen.

Stijn van Liefland

Piketty for dummies (4)

In de eerste blog in deze serie is de eerste hoofdwet van Piketty behandeld en in de tweede blog de tweede hoofdwet. Vervolgens hebben we cijfermatig het model van Piketty met de twee hoofdwetten verkend in wat simulaties. We weten nu hoe op lange termijn de inkomensverdeling tot stand komt. De belangrijkste conclusie was dat historisch bezien de vergoeding op kapitaal zo rond de 5% zit en de groei van de economie zo rond de 1,5-2% zit. Door de beschreven wetmatigheden krijg je dan onvermijdelijk dat het arbeidsdeel van het totale inkomen wordt weggedrukt door het kapitaalsdeel.

Toch heeft het iets onbevredigends. De hele redenering draait ‘in the end’ om drie kernvariabelen:

De vergoeding op kapitaal (de rente r).
De spaarneiging (s).
De groei van de economie (g).

Hoe worden deze variabelen nu eigenlijk bepaald? Piketty gaat hier jammer genoeg slechts kort op in. Misschien aardig om er hier eens wat langer bij stil te staan.

De vergoeding op kapitaal

Piketty laat overtuigend zien dat de vergoeding op kapitaal over alle tijden en landen heen altijd zo rond de 5% ligt. Soms wat lager en soms wat hoger. En uiteraard voor de ene belegging met meer risico een hogere vergoeding dan voor de andere die een lager risico kent. Maar toch. Waarom toch die 5%?

Het makkelijkste en meest intuïtieve verhaal vind ik het dak boven je hoofd dat iedereen nodig heeft. Om een huis te bouwen inclusief grond ben je (minimaal) zo’n € 100.000 kwijt. Voor minder iets fatsoenlijks bouwen wordt echt lastig. Wat ben je kwijt per maand om zoiets te kunnen of mogen bewonen? Als je gaat huren dan betaal je hoe dan ook al snel € 400 per maand. Dat is ongeveer € 5.000 per jaar. Met andere woorden: als ik € 100.000 aan geld over heb en ik zou een huis bouwen als belegging (om een ander daarin te laten wonen) dan mag ik rekenen op een jaarlijkse vergoeding van € 5.000 oftewel een rendement van 5%. Misschien moet ik wat meer vragen voor eventueel onderhoud en verzekeringen of krijg ik effectief (na aftrek van onderhoudskosten) een iets lagere vergoeding.

Interessant is dan om na te denken over een technologische ontwikkeling die het mogelijk maakt om voor pak hem beet de helft van dit bedrag een goed huis te bouwen. Zou je dan een lagere structurele vergoeding op je kapitaal krijgen? Klinkt niet onlogisch: een hogere en efficiëntere techniek in het bouwen zorgt ervoor dat je meer kunt consumeren en minder hoeft te sparen. Dat is dus minder vraag naar kapitaal en zorgt voor een lagere rente. Maar je hebt altijd nog de grond onder je huis nodig en grond is eindig en dus schaars.

Een andere invalshoek is de schaarste van kapitaal. Een kwestie van vraag en aanbod. Het voorbeeld hierboven geeft al aan dat bij een efficiëntere bouwtechniek minder vraag naar vermogen (voor huizenbouw) ontstaat. Maar je hebt voor een investering ook energie nodig en grondstoffen. Energie wordt nog vooral gemaakt uit eindige voorraden olie en ook (andere) grondstoffen zijn vaak eindig. Hoe dan ook zal vermogen dat je stopt in eindige voorraden (die nog nodig blijven) een bepaald rendement afdwingen vanuit de schaarste. Populair gezegd: ik weet dat een eindige voorraad grondstof veel waard is (of wordt) en ben dus bereid een deel van die voorraad te kopen. Dan wil ik dus ook geld van een ander lenen en daar een vergoeding voor betalen omdat ik weet dat ik dat op termijn terug kan verdienen.

Duidelijk is dat in een wereld waarin nauwelijks schaarste bestaat (voldoende grondstoffen, land en energie) een lagere rente zal ontstaan. Een rente van 5% is een weerspiegeling van de eindigheid en de schaarste van grondstoffen, land en energie (en van onze levens, maar zie hieronder).

De spaarneiging

De keerzijde van een vergoeding op kapitaal is de neiging om te willen sparen. Waarom zouden we überhaupt sparen? Is het niet beter om gewoon alles wat je verdient lekker op te maken? Dat is wat veel dieren ook doen: ze gaan op jacht als ze honger hebben en eten dan wat ze nodig hebben. Wat hier speelt is dat mensen a) eindig leven, en b) vooruit (kunnen) kijken. Dat ze eindig leven betekent dat er altijd een kans is dat als ze een deel van hun inkomen nu niet opmaken, dat ze dan de volgende periode daar alsnog niet meer van kunnen genieten (omdat ze dood zijn of ziek of het wordt gestolen of het is bedorven). Dat ze vooruit kijken betekent dat ze ook nadenken over hun toekomst. Als ze nu een bepaald inkomen hebben en eventueel een deel opzij kunnen zetten, dan betekent dat dat ze voor morgen minder risico lopen. Ook als het inkomen dan tegenvalt, hebben ze toch nog wat te eten. Hoe dan ook sparen en dingen opzij zetten, heeft een nuttige functie.

De neiging tot sparen leidt dus tot opbouw van kapitaal. In combinatie met wat ik onder ‘de vergoeding van kapitaal’ heb gesteld ontstaat er nu een mogelijke uitruil tussen vragers en aanbieders van kapitaal. De een wil afzien van consumptie in het heden (sparen), de ander wil ‘vooruit consumeren’ (investeren, bijvoorbeeld door een huis neer te zetten). Op deze manier kan er onderling worden onderhandeld over een vergoeding die voor beiden interessant is.

Een ingewikkelde manier om te zeggen dat de rente tot stand komt in een markt van vraag en aanbod. Rente en kapitaal/vermogen maakt het mogelijk om in de tijd tot optimale keuzes te komen. Een hogere rente betekent dat meer mensen bereid zullen zijn hun consumptie uit te stellen en minder mensen bereid zullen zijn een huis te gaan bouwen.

Zo komen we tot de stelling dat de eindigheid van het leven van mensen (waar de tijdsvoorkeur uit ontstaat, de neiging consumptie in het heden hoger te waarderen dan een onzekere consumptie in de toekomst) enerzijds en de eindigheid van grondstoffen en energie anderzijds, in onderlinge wisselwerking de vergoeding op kapitaal bepaalt. Hoe hoger de neiging tot sparen (hoe lager de tijdsvoorkeur) hoe lager de rente zal zijn. Je zou ook kunnen stellen dat hoe ouder mensen worden (én daarbij ook gezond en werkzaam kunnen blijven) hoe lager de rente zal zijn.

Opmerkelijk is dat deze complexe wisselwerking op de kapitaalmarkt altijd tot vergoedingen van zo’n 5% heeft geleid (stelling Piketty).

De spaarneiging is ook al zo’n constante, zo rond de 10-12%. Hier speelt cultuur van een volk mogelijk wel een rol. Een spaarzaam land als Japan laat een hogere spaarneiging zien dan een land dat makkelijker consumeert en leent als de VS (14% resp 7-8%).

De groei van de economie

Dan houden we nog maar één variabele over. De groei van de economie. En als we de andere twee al weten dan volgt deze eigenlijk vanzelf (zie de twee hoofdwetten). Dus de eindigheid van onze levens en de schaarste aan eindige grondstoffen en energie zorgt ervoor dat we structureel niet veel harder kunnen groeien dan 1,5-2%.

Er zijn een paar zaken die dit kunnen veranderen. De vondst van nieuwe voorraden bijvoorbeeld. Als plots een nieuwe wereld aan grondstoffen wordt ontdekt dan maakt dat extra groei mogelijk (en zal de vergoeding op kapitaal ook navenant lager worden). Verder de uitvinding van nieuwe technieken die de efficiency van productie en consumptie verhogen. En als we als menssoort slimmer en handiger worden. Allemaal voorbeelden die erop neer komen dat onze ‘productiefunctie’ beter wordt en ons dus in staat stellen meer te doen met minder middelen.

Blijkbaar is het structureel nog niet mogelijk gebleken zoveel uitvindingen te doen (of te investeren in steeds meer opleiding) dat we meer dan een eeuw boven de 3-4% groei uit kunnen komen. Niet raar want door het groei op groei effect (exponentieel verloop) raakt de voorraad grondstoffen steeds sneller uitgeput en/of wordt land in combinatie met een steeds sneller zich verdubbelende bevolking steeds schaarser.

Terug naar ongelijkheid

We moeten vanuit dit nieuwe inzicht terug naar de basisvraag van Piketty. Als uit historische cijfers blijkt dat r > g, dan leidt dat automatisch tot een steeds hoger aandeel van rente-inkomsten en dus tot een verdrukking van inkomen uit arbeid. Maar dat moet dan toch een tegenbeweging uitlokken en tot een nieuw evenwicht leiden?

Stel dat de groei helemaal afvlakt en naar 0% gaat. Zeker niet ondenkbaar voor de komende 50 jaar. De spaarneiging is 10% en zal wellicht wat zakken naar 8% (maar helemaal 0% kan het nooit worden). Dan zal beta (vermogen/inkomen ratio) naar oneindig gaan. Oftewel het vermogen zal duizenden keren hoger zijn dan het totale (gelijkblijvende) inkomen. Maar wat gebeurt er met dat vermogen? Daar is toch helemaal geen vraag naar? Waar moet je immers in investeren of beleggen? De rente zal onherroepelijk dalen want er is een overschot aan kapitaal (en een tekort aan nieuwe aanwendingen voor dat kapitaal).

Dus hoe zit dat dan? Daarover meer in de volgende blog.

Rudy van Stratum

Tegendenken (19): Rituelen

Als het zo lastig is om het persoonlijke en inhoud uit elkaar te houden wat kunnen we daar dan aan doen? Alles anoniem maken is een mogelijkheid, ook de verplichting om tegenargumenten te noemen kan helpen. Immers als je verplicht bent op zoek te gaan naar tegenargumenten dan doe je dat omdat het moet en niet omdat je iemand wilt afzeiken. Eigenlijk zou je op zoek moeten naar nieuwe rituelen die je gebruikt om tegendenken een plek te geven. Bijvoorbeeld, als er in een vergadering een nieuw idee of plan wordt gepresenteerd maken we een rondje en moet iedereen een (of twee) tegenargument inbrengen. Dat kan mondeling maar misschien zou het nog beter zijn dit schriftelijk te doen. Lastig is wel dat je voor je het weet een enorme discussie krijgt, een goed en helder format is daarom wel zo handig.

Een methode die ik tegenkwam tijdens onze zoektocht is “ritual dissent” (ritueel afwijken). Bij een plan, idee, voorstel, strategie of wat dan ook kan je deze methode gebruiken om tot verbetering te komen. Het gaat als volgt.

Je nodigt een groep mensen uit om in een workshop-achtige setting jouw voorstel te bespreken. Volgens de bedenkers zouden dat vooral veel mensen van buiten moeten zijn. Dat is ongetwijfeld goed, maar als je dit vaak wilt doen wel lastig te organiseren. Ik denk dat het ook in een vergadering met collega’s moet kunnen of zelfs binnen een projectgroep, maar het is wel handig als er mensen met een verschillende achtergrond bij zitten. Uiteraard krijgen deze mensen (de critici) een korte introductie op het doel en een uitleg van de methode en de bijbehorende regels.
De inbrenger houdt een korte presentatie over het achterliggende probleem en het idee (voorstel plan etc.) dat dit probleem moet oplossen. De critici luisteren aandachtig maar geven geen commentaar.
Vervolgens draait de inbrenger zich om en gaat met de rug naar de critici zitten. De toehoorders bekritiseren vervolgens het idee zonder enige remming. Ze geven allerlei redenen waarom dit idee niet gaat werken en komen met alternatieven die het probleem beter oplossen. De inbrenger hoort aan wat er gezegd wordt en maakt aantekeningen.
Na het leveren van de kritiek krijgt de inbrenger wat tijd om zijn / haar gedachten te ordenen. Vervolgens draait hij zich weer om en vertelt wat hij / zij geleerd heeft. Noch de inbrenger noch de toehoorders hoeven zaken verder toe te lichten of te verantwoorden. De inbrenger neemt het geleerde mee en gaat er mee aan de slag (of besluit om met het idee te stoppen).

Een wat uitgebreidere vorm is om in een dagdeel meerdere problemen / ideeën te bespreken in verschillende groepen waarbij het idee / probleem steeds weer in een nieuwe groep besproken wordt.

Niet alleen maakt deze methode van het leveren van kritiek een ritueel, ook legt het de focus op luisteren naar de inhoud. Soms zal wel duidelijk zijn wie het zegt, maar de mimiek, de houding en de non-verbale reacties van anderen blijven allemaal achterwege.

Stijn van Liefland

Tegendenken (18): Persoon en inhoud

Het lastige van tegendenken is dat kritiek vaak gekoppeld wordt aan de persoon. Dat werkt twee kanten op. Degene die kritiek levert kan gezien worden als die lastige persoon en dat is vaak niet fijn, zeker niet als de bedoelingen goed zijn. Maar ook voor degene die de kritiek ontvangt is het vaak persoonlijk. Want kritiek op een plan (waar je lang aan gewerkt hebt en wat veel voor je betekent) kan al snel opgevat worden als kritiek op de persoon. Van kritiek op de inhoud maak je in je hoofd al snel de bruggetjes naar, “hij vindt dat ik niet mijn best heb gedaan” … “hij vindt dat ik nooit wat goeds doe”… “ik deug niet als mens”. Rudy heeft al eerder twee blogs geschreven over “ja maar (1)” (ja maar 2). Kort door de bocht: ja … (lees, ik zie jou als persoon wel zitten), maar … (lees, dit idee lijkt me nou niet zo goed). Het is een manier om de persoon te waarderen en kritisch te zijn naar de inhoud. Nadeel is dat het vaak verwarrend is. “Je zei ja, je vond het dus een goed plan”.

Wat het vooral lastig maakt is dat je als persoon meestal onderdeel bent van een groep. Als jouw kritiek dus persoonlijk wordt opgevat (of als je dat doet bij de kritiek van een ander) dan beïnvloedt dat jullie relatie terwijl je als groep nog verder moet. Dan kan je iemand van buiten de groep halen, bijvoorbeeld een adviseur. Maar die krijgt ook een relatie met de groep en heeft ook een belang. Stel dat je als adviseur goede kritiek geeft maar daardoor vindt iedereen je een rotzak dan is de kans klein dat je nog eens ingehuurd wordt. Denk nou niet dat die goede kritiek blijft hangen, iedereen zal het gevoel hebben dat de groep dat zelf heeft gedaan. Wat blijft hangen is die irritante adviseur die maar bleef drammen en op alle slakken zout legde.

Kritiek geven en kritiek ontvangen is dus lastig. Bij de beleving van die kritiek speelt nogal wat mee zoals bijvoorbeeld:

De persoon die het geeft (onze ervaringen en onze vooroordelen daarover)
De toon
Het volume
De mimiek
De houding
Het moment waarop het gebracht wordt
Het taalgebruik, specifieke woorden
De ontvanger (zijn / haar verleden, hoe die nu in z’n vel zit etc.)

en dan ben ik vast niet volledig*. Dit speelt allemaal een rol bij hoe we de kritiek opvatten die vaak helemaal niet persoonlijk bedoeld is. Soms wordt er ook bijgezegd dat je het niet persoonlijk moet opvatten. Ja, dan weet je het wel, dan wordt het echt persoonlijk. Want eigenlijk is dat net zoiets als zeggen “jij kunt niet met kritiek omgaan” en dat gaat dus over hoe jij als persoon bent.

Helemaal uitschakelen kan je de persoonlijke component niet maar er zijn wel hulpmiddelen. Je kunt bijvoorbeeld alles schriftelijk en anoniem afdoen, maar dat is nogal omslachtig. Een andere manier is om allemaal tegelijk kritiek te leveren. Als iedereen het doet en zelfs moet doen, dan gaat het persoonlijke er wel van af. De komende afleveringen gaan we wat technieken bespreken die helpen bij tegendenken.

Stijn van Liefland

*Eigenlijk gaat het hier om non-verbale communicatie die soms net zo belangrijk is als de verbale, maar verwarrend als de inhoud centraal staat. We komen hier laten nog een keer op terug.

Piketty for dummies (3)

Even wat spelen met de cijfers. We gaan uit van de basissituatie zoals door Piketty genoemd. Ik verwijs naar de eerdere blogs over de 2 hoofdwetten.

Het nationale inkomen NI = 30.000 per jaar. De kapitaalgoederenvoorraad CAP = 180.000 per jaar. De vergoeding op kapitaal R=5%. Het groeipercentage van de economie G=2%. Het spaarpercentage S=12%. Beta geeft de kapitaal-inkomensverhouding weer, door Picketty in 2010 op ongeveer 6 ingeschat. Alfa geeft het aandeel van kapitaal in het nationaal inkomen weer en is gesteld op 30%.

Het basisscenario

Hier zie je mooi dat bij een groei van 2% van de economie alle verhoudingen netjes constant blijven.

Een groei van 0%

Benieuwd wat er gebeurt als de groei tot stilstand komt?

Nu zie je inderdaad dat het kapitaalsaandeel in de economie steeds groter wordt. Er blijft op termijn niets meer over voor beloning voor arbeid. Deze situatie is zelfs instabiel omdat er geen einde zit aan de hoogte van beta (delen door 0 mag niet!) en uiteindelijk zou LI zelfs negatief worden (wat in dit modelletje niet is toegestaan natuurlijk). Maar het idee is duidelijk: een zekere groei van de economie is nodig om tegenwicht te bieden aan de rentevergoedingen op kapitaal.

Een groei van 3%

Wat gebeurt er als we aannemen dat de economie wat sneller groeit (maar minder snel dan het rentepercentage)?

Nu kun je zien dat bij een groei van 3% het kapitaalsaandeel zal dalen. En dat ondanks dat de vergoeding op kapitaal R=5%. Volgens de formule/hoofdwet beta = s / g zal beta verder blijven dalen en langzaam naar de waarde van 4,00 gaan. De alfa gaat langzaam naar de waarde van 0,20. Je ziet hier het bewijs dat r > g geen probleem hoeft te zijn. Alleen mag het verschil tussen r en g niet te groot worden (in deze rekenvoorbeeldjes mag de groei van de economie dus niet meer dan 3%-punten onder de vergoeding op kapitaal liggen).

Rente omhoog

Met hoeveel moet de rente dan stijgen om bij een hogere groei van 3% toch weer een beta van 6 te krijgen? Nou, dat gaat dus niet lukken. Ik heb een hele hoge rente genomen van 10%. De beta zal op termijn toch weer gewoon naar de waarde 4 gaan (s/g namelijk, die is niet afhankelijk van r). Maar de alfa zal op termijn hoger eindigen (start ook flink hoger) op een waarde van 0,40 (namelijk r x beta).

Genoeg gepield met de formules en getallen van Picketty. Hopelijk is er zo wat gevoel ontstaan bij de logica achter de hoofdwetten. Probleem blijft dat dit rekenmodel een aantal zaken fixeert (exogeen veronderstelt) die eigenlijk zelf ook weer verklaard moeten worden. Als we dat ook gaan uitwerken (wat op zich prima kan) dan krijgen we een compleet economisch model en verlaten we de bespreking van Picketty. Toch ga ik in de volgende blog in woorden (zonder formules) wel in op de mogelijke verbanden.

Rudy van Stratum

Voor de liefhebbers hier het totale rekenmodelletje met de 2 hoofdwetten:

(1) NI = NI(-1) . (1+g)

(2) SAV = s. NI

(3) CAP = CAP(-1) + SAV

(4) CI = r . CAP

(5) LI = NI – CI

(6) alfa = CI / NI ( via substitutie van (4) en (7) in (6) volgt dat alfa = r . beta, hetgeen de 1e hoofdwet vormt)

(7) beta = CAP / NI

De tweede hoofdwet (beta = s / g) heb ik noch Picketty in zijn boek afgeleid (wat lastiger!) en geldt niet altijd op elk moment en wordt in de simulaties hierboven wel duidelijk zichtbaar op de langere termjin.

Piketty for dummies (2)

In de vorige blog over het recente werk van Piketty ging het over de eerste hoofdwet van kapitaal en groei. In deze blog staan we stil bij de tweede hoofdwet.

De tweede hoofdwet is minder makkelijk af te leiden en dat is iets wat Piketty zelf ook niet expliciet doet. Er zijn aanvullend relaties van belang:

CAP = CAP (-1) + SAV

Hier staat dat de nieuwe hoeveelheid kapitaal gelijk is aan de oude voorraad kapitaal plus wat je toevoegt door besparingen (op het totale inkomen).

NI = (1+g) . NI (-1)

Hier staat dat het totale verdiende inkomen (of de jaarlijkse output van de economie) jaarlijks groeit met een percentage g.

SAV = s. NI

Hier staat dat de besparingen SAV een deel s van het inkomen (NI) uitmaken. Voor het gemak van interpretatie mag je er hier vanuit gaan dat het alleen de eigenaren van vermogen zijn die sparen.

Nu kun je aantonen (ook door gebruik te maken van de eerste wet) dat op langere termijn (na een flink aantal jaren, denk aan 40-50 jaar) geldt dat het aandeel van het kapitaalinkomen op het totale inkomen (beta) wordt bepaald door:

beta = s / g

Dit is wat Piketty de tweede hoofdwet van kapitaal en groei noemt.

Merk op dat de eerste hoofdwet een definitie-kwestie is (die klopt altijd en overal) en dat deze tweede hoofdwet een benadering voor de langere termijn is (dus niet precies en niet op elk moment geldig). Ik zal in de volgende blog het complete modelletje met de 2 hoofdwetten nog eens uitschrijven en met cijfers in de tijd illustreren op de werking ervan.

Interpretatie

Naarmate je meer spaart (een hogere s) maak je minder op en voeg je meer toe aan je voorraad kapitaal. Dat betekent dat door de jaarlijkse vergoeding op kapitaal van r% het kapitaalsaandeel jaar op jaar groter wordt. Oftewel: het aandeel van de totale output dat naar arbeid gaat wordt steeds kleiner. Dat klinkt logisch: veel sparen betekent veel vermogen en dat betekent veel rente-inkomsten en dan hoef je minder te werken.

De andere is wat lastiger. Naarmate de economie minder hard groeit (een lagere g) zal het aandeel kapitaalinkomen (CI) op het totaal groter worden. Dit is eigenlijk een schuldenprobleem. Elk jaar dat er geen groei is zal de voorraad kapitaal toch groeien door de aanwezigheid van r% rendement en op die manier de rest van het inkomen verdringen. Alleen een flinke groei is in staat om de jaarlijkse rente-betalingen te compenseren en weer te werken aan het arbeidsdeel van het totale inkomen.

We kunnen nu ook globale getallen gaan invullen om het duidelijker te maken. Van de beta wisten we al dat die momenteel in het Westen rond de 6 zit. De spaarquote blijkt historisch ook redelijk constant te zijn. Voor een land als Japan is de spaarquote aan de hoge kant, zo rond de 14%. Voor een land als de VS zit de spaarquote aan de lage kant, zo rond de 7-8%. Maar gemiddeld ligt de spaarquote zo ergens tussen de 10 en 12%.

Als we in de formule van de tweede hoofdwet hierboven dan voor beta = 6 invullen en voor s = 12% dan volgt vanzelf het langere termijn groeipercentage van de economie. En die blijkt dan uit te komen op een jaarlijkse groei van 2%.

Dus: 6 = 0.12 / 0.02

En nu komen we zoetjesaan bij wat volgens mij een van de hoofdstellingen van Piketty is.

De groei op lange termijn is laag!

Uit de historisch analyse van Piketty blijkt dat de economie gemiddeld over heel veel jaren bekeken niet zo snel groeit of kan groeien. Over de periode 0-1700 is sprake van nagenoeg stilstand of nulgroei. Over de periode 1700-2012 is gemiddeld sprake van een groei van 1,6%. Eigenlijk is een lage groei de regel en een hogere groei uitzondering. Laag is dan 0-2% en hoog alles daarboven. Een uitzonderlijke periode van hogere groei is de periode na de tweede wereldoorlog tot ongeveer 1970.

Laten we dat eens bekijken in het licht van dé grote uitspraak van Piketty: r > g. Als de situatie aan de hand is dat r (de vergoeding op kapitaal) hoger is dan g (de groei van de economie) dan moeten in het kader van groeiende ongelijkheid de alarmbellen gaan rinkelen.

Als we op deze manier naar de laatste 300 jaar kijken dan krijg je globaal:

1700-1910: lage groei van de economie en dus een toename van de ongelijkheid (groot aandeel kapitaalinkomen in totale inkomen).

1910-1950: diverse correcties, 2 wereldoorlogen, financiële crisis 1929, veel vernietiging van kapitaal.

1950-1970: historisch uitzonderlijke periode van hoge economische groei door wederopbouw en inhaalslag, historisch bezien relatief grote gelijkheid.

1970-2010: weer terug naar lagere groei, oliecrisis, financiële crisis 2008, toename van ongelijkheid.

Waar het op neerkomt is dat de vergoeding op kapitaal historisch gezien zo rond de 5% ligt en dat de groei van de economie structureel niet hoger ligt dan 1,5-2%. Oftewel, nagenoeg altijd geldt dat r > g hetgeen betekent dat er altijd een druk is op de inkomensverdeling. De vergoeding op kapitaal heeft inherent de neiging het arbeidsinkomen te verdrukken.

Structureel een hoge groei is door de groei-op-groei situatie nagenoeg onmogelijk. We zouden in no-time op een vertienvoudiging van de huidige bevolking en/of output zitten. Het is daarom voor de 21e eeuw zeer onwaarschijnlijk van een hogere groei uit te gaan. Een hoge groei is dus tijdelijk en uitzonderlijk. Een situatie van oorlog zorgt daarna voor een groeispurt in verband met wederopbouw. Dat verklaart de hoge groei van ná 1945. Verder is een hoge groei zichtbaar in specifieke delen van de wereld die een inhaalslag maken zoals China ná 1990. Maar nogmaals: dat zijn de uitzonderingen die de regel van lage groei bevestigen (aldus Piketty).

Onbevredigend

De analyse tot dusver is onbevredigend omdat het hele verhaal draait om drie grootheden waarvan we eigenlijk niet goed weten hoe ze worden bepaald.

– De groei van de economie, waar hangt die vanaf, hoe komt die tot stand?

– De vergoeding op kapitaal (de rentevoet), waar is die van afhankelijk?

– De spaarquote, hoeveel willen of kunnen we sparen en waar wordt dat door bepaald?

En dan nog: deze variabelen zijn deels van elkaar afhankelijk. Dus hoe zit het nu? Daar gaan we in een latere aflevering op in.

In de eerstvolgende blog ga ik als tussenstap wat spelen met het modelletje van Picketty. Zo krijgen we wat gevoel voor de hoofdwetten en snappen we beter hoe het werkt.

Rudy van Stratum

Is windenergie te duur?

Deze week vond ik een aardig publicatie over windenergie, “argumenten bij 5 stellingen”, op de site van het planbureau voor de leefomgeving. Aanleiding is de doelstelling om in 2020 14 procent hernieuwbare energie te gebruiken die binnen de EU is afgesproken. Het Energieakkoord kijkt naar 2023 en heeft de ambitie om 16 procent te realiseren. Het coalitieakkoord bevat een doelstelling van een volledig duurzame energievoorziening in 2050 en de Europese ambitie voor 2050 is om 80-95 procent reductie van broeikasgassen te
realiseren. Hiervoor zal veel duurzame energie opgewekt moeten worden. In het Energieakkoord wordt daarom hoog ingezet op windenergie.

Het gaat om de volgende 5 stellingen:

Windenergie is niet nodig, er zijn betere alternatieven (klopt niet)
Windenergie levert geen CO2-reductie op (klopt niet, jammer is wel dat windenergie vooral relatief schone elektriciteit, opgewekt door gas verdringt)
Windenergie past niet in Nederland: we zijn te dicht bevolkt (klopt deels, ligt genuanceerd)
Windenergie is te duur (hier ga ik verder op in).
Windenergie biedt economische kansen (klopt redelijk).

Het is jammer dat de auteurs zich vooral beperken tot de argumenten en niet met een conclusie komen. De conclusies (tussen haakjes) heb ik daarom zelf maar getrokken op basis van het stuk.

De stelling dat windenergie duur is, is natuurlijk een interessante om hier verder te behandelen. Ik ga daarbij in dit eerste artikel volledig uit van de tekst in de publicatie en probeer die samen te vatten en wat te verhelderen. Maar vooraf is het interessant om even stil te staan bij de vraag wat te duur betekent? Is windenergie te duur als het duurder is dan bijvoorbeeld energie uit kolen? Of is windenergie te duur als niemand het wil hebben? Ik trek maar even de vergelijking met een simpel willekeurig product als een zomerjas, wanneer is die te duur? Volgens mij als niemand die jas wil kopen voor de gevraagde prijs. Het zou dus interessant zijn te weten wat mensen bereid zijn te betalen voor bijvoorbeeld windenergie van zee, dan weten we wanneer het te duur is. Maar goed, grote kans dat veel mensen niet meer willen betalen dan ze nu betalen, dat is ook het uitgangspunt van deze studie, een vergelijking met de huidige prijzen. De auteurs geven niet aan wat ze met te duur bedoelen, ik ga er daarom van uit dat de stelling is, windenergie is te duur, het kan op basis van financiële argumenten niet concurreren met andere energiebronnen.

Windenergie is te duur
Windenergie op gunstige locaties op land is nagenoeg concurrerend met fossiele stroom. Op minder gunstige locaties nog niet. Maar wat niet is kan nog komen, de afgelopen 30 jaar zijn de kosten voor windenergie jaarlijks met gemiddeld 5% gedaald, als die daling doorzet wordt het ook op andere plekken al snel concurrerend. Anders ligt het met windenergie op zee, die is 2 tot 3 keer zo duur als fossiele stroom. Om de doelstellingen te halen wordt de komende jaren juist fors ingezet op windenergie op zee. Is windenergie op zee dan te duur of gaat hier de komende jaren nog veel veranderen waardoor het wel concurrerend wordt?

In het energieakkoord is het doel opgenomen dat de komende 10 jaar de kosten voor windenergie op zee met 40% gaan dalen. Door deze daling is windenergie op zee nog steeds duurder dan fossiele stroom en windenergie op land. Maar deze hebben beide hun nadelen. Het Rijk wil windenergie op zee dan ook subsidiëren mits deze kostenreductie gerealiseerd wordt. Op zich een slimme aanpak, want een subsidie heeft als risico dat het partijen lui maakt en daardoor innovatie tegenwerkt, dat voorkom je hiermee.

Bij die prijsdaling van 40% zitten een paar adders onder het gras. Een belangrijke is dat windmolens die verder op zee staan duurder zijn. De zee is dieper, en dus is er meer materiaal nodig en is plaatsing lastiger en omdat het verder weg is heb je een langere kabel nodig en wordt onderhoud ook een stuk duurder. Maar de keuze voor de locatie is vooral een planologische kwestie en je kan de kosten voor windstroom daarvoor corrigeren. Het zou zo in theorie kunnen dat windenergie op zee 40% goedkoper is geworden maar als gevolg van planologische keuzes je daar weer een hoop van inlevert. Het Rijk houdt hier bij de subsidiëring rekening mee. Nog een addertje heeft te maken met vraag en aanbod van elektriciteit als er heel veel windenergie wordt aangeboden dan daalt op dat moment de elektriciteitsprijs en wordt windenergie dus vanzelf minder rendabel. Misschien komen we daar later nog wel op terug.

Uitgaande van die prijsdaling is het interessant is te kijken naar de prijsontwikkeling van windenergie op zee in de afgelopen jaren. In 2006 en 2008 werden in Nederland 2 windparken geopend, daarna zijn de prijzen niet gedaald maar gestegen:

Windparken worden verder uit de kust aangelegd.
De eerste windmolens op zee waren daar niet voor bedoeld en konden niet goed tegen de omstandigheden. De nieuwe molens wel, maar deze zijn daardoor wel duurder. De kWh prijs van deze nieuwe molens is uiteindelijk lager. Het lijkt mij dat kosten per kWh over een langere periode uiteindelijk bepalend zijn, ik zou dit dus als kostenverlagend zien.
Bedrijven wilden zich graag ontwikkelen op de markt voor windenergie op zee en leverden relatief goedkoop met lage winstmarges (bijvoorbeeld offshore bedrijven). Nu willen ze een normale winst.
Windmolenfabrikanten hadden veel werk aan windenergie op land en konden door schaarste aan molens hogere prijzen rekenen.
De prijzen voor grondstoffen zoals koper en staal zijn flink gestegen. Inmiddels zijn de prijzen weer gedaald maar nog tot het oude niveau.

Offshore parken die na 2006 gebouwd werden waren daardoor 2 keer zo duur als parken daarvoor. Maar de verwachting is dat bovengenoemde factoren in de toekomst geen rol meer spelen. De keten van leveranciers is nu een stuk stabieler.

Los van de prijsontwikkeling in het verleden is een belangrijke vraag of het lukt om in 10 jaar de kosten met 40% te verlagen. Het is interessant te kijken hoe dit aangepakt wordt.
Aan de ene kant is er een leercurve waarmee je de verlaging van de kosten kunt bepalen bij elke verdubbeling van de capaciteit. Hierbij wordt er vanuit gegaan dat een verdubbeling van het vermogen van windenergie op zee tot een leereffect leidt dat vervolgens weer leidt tot een kostenbesparing. In dit geval 5 -9% kostenbesparing bij verdubbeling. Hierbij wordt geen rekening gehouden met externe factoren (zoals grondstofprijzen) die dit weer teniet kunnen doen.
Een ander manier is een meer technische kijk, de hele keten analyseren en onderzoeken waar mogelijkheden liggen voor besparing. Die zijn er, een kostendaling van 30-40% is mogelijk, maar een kostendaling van 40% in 10 jaar wordt als zeer ambitieus gezien.

Tegendenken
Nu wordt het even tijd voor tegendenken. Als je iemand in zeg 2002 had gevraagd hoe de prijzen voor offshore windenergie zich zou ontwikkelen zou die waarschijnlijk zeggen dat de prijs naar beneden zou gaan (ik heb het overigens niet gecontroleerd). Vervolgens blijken er allerlei factoren te spelen die je vooraf niet had zien aankomen (weerstand tegen parken nabij de kust, prijsstijgingen van grondstoffen, marktmechanismes etc.). Op dit moment concluderen we dat deze factoren de komende jaren niet meer van belang zijn. Dan vraag ik me twee dingen af. ten eerste waarom zouden deze factoren over een paar jaar niet opnieuw een rol spelen en ten tweede, welke andere onvoorziene factoren komen er nog op ons af? Zonder enige kennis of studie noem ik maar even een paar punten die me zo te binnen schieten:

Extra veiligheidsmaatregelen (in oktober 2013 overleden twee monteurs in een molen a.g.v. Brand)
Extra voorzieningen t.b.v. vogels of veiligheid van de scheepvaart.
Stijging van de kosten om windmolens te plaatsen. Door de aantrekkende economie hebben offshore bedrijven weer de handen vol aan de olie- en gasindustrie.
Etc.

We hebben al eens eerder verwezen naar het boek zwarte zwanen van Taleb, verwacht het onverwachte.

Hoe zit het met de opbrengst?
Als het gaat om de vraag of windenergie duur is en vooral of het kan concurreren met andere energiebronnen, dan heb je aan de ene kant de kosten en aan de andere kant de opbrengsten. De kosten zijn hoog zoals hierboven is beschreven. De opbrengsten komen uit de verkoop van elektriciteit en zijn dus een gevolg van de op dat moment geldende prijzen. Nou is het lastige bij windenergie dat het aandeel over een heel jaar beperkt kan zijn maar op bepaalde momenten heel hoog. Als er weinig vraag is en het waait hard (bijvoorbeeld ’s nachts) dan kan het aandeel windenergie op dat moment relatief hoog zijn. In Denemarken en Duitsland heeft deze situatie zich al voorgedaan. Het gevolg is dat op dat moment het aanbod aan elektriciteit een stuk hoger ligt dan de vraag en de vergoeding per geproduceerde kWh dus laag wordt. Je zou zelfs kunnen zeggen dat naarmate windenergie een groter succes wordt, de vergoeding per geleverde kWh naar beneden gaat. Alleen oplossingen op systeemniveau zoals energieopslag of uitwisseling van elektriciteit met landen ver weg kan hier voor een oplossing zorgen.

Conclusie
We komen hier nog een keer op terug met meer kritische beschouwingen, maar dat vraagt nog wel wat denkwerk. Voorlopig is mijn conclusie windenergie op land is niet duur, windenergie op zee is wel duur. Ik had het graag anders gezien maar loop de beredenering nog even door.
Windenergie op land is nagenoeg concurrerend. Je mag aannemen dat nieuwe molens een wat hoger financieel rendement hebben zodat dit op korte termijn echt concurrerend is.
Windenergie op zee is ongeveer 2 keer zo duur als windenergie op land. Het energieakkoord hoopt op een kostenreductie van 40%. Het is twijfelachtig of je deze kostenreductie haalt. Op basis van de leercurve verwacht je het niet, op basis van een meer technische benadering zou het kunnen maar is het zeer ambitieus. Daarbij is dan geen rekening gehouden met allerlei onverwachte ontwikkelingen. En, bij een kostenreductie van 40% is het nog steeds duurder dan wind op land wat nagenoeg (maar dus niet helemaal) concurrerend is.

Waar we het dan niet over gehad hebben zijn allerlei externe effecten. Welke externe kosten en besparingen heeft windenergie op zee t.o.v. fossiele energie en welke neveneffecten treden er op zoals bijvoorbeeld marktkansen voor Nederlandse bedrijven. Windenergie op zee zou dan rechttoe rechtaan berekend duurder kunnen zijn, maar over de langere termijn, met een bredere blik op rendement wellicht best aantrekkelijk. Of niet, dat kan er natuurlijk ook uitkomen.

Stijn van Liefland

Piketty for dummies (1)

Het kan bijna niet missen of je hebt de afgelopen maand de naam Piketty een keer gehoord. Thomas Piketty is Frans econoom en auteur van een volgens velen baanbrekend boek over economische ongelijkheid. Zie voor meer achtergronden het artikel van Rutger Bregman op De Correspondent. Het boek (dat eind van dit jaar in een Nederlandse vertaling verschijnt) is grofweg in te delen in een ‘feitelijk’ deel en in een ‘opiniërend’ deel. Dat tweede deel gaat over de mogelijke toekomsten van onze economieën in deze eeuw en bevat aanbevelingen over hoe we extreme ongelijkheid via (met name belastingmaatregelen) kunnen voorkomen.

Mijn idee was om het eerste deel van zijn boek in enkele blogs uiteen te zetten. Dat eerste deel vormt als het ware het skelet van de redenering van Piketty en is handig om (mocht je het boek zelf nog willen gaan lezen) het sneller te lezen of beter te begrijpen.

Deze eerste blog gaat over de zogenaamde eerste wet van kapitaal en groei.

De eerste wet van kapitaal en groei

Een economie maakt elk jaar een hoeveelheid producten en diensten. Dit wordt de output of productie van de economie genoemd. Ik ga even voorbij aan allerlei subtiliteiten en stel dat de totale productie van een economie gelijk is aan het totale inkomen (van de bevolking) in dat jaar. We noemen dat totale inkomen NI (van nationaal inkomen).

Dat NI (nationale inkomen) gaat uiteindelijk ófwel naar arbeid ófwel naar kapitaal. In het geval van arbeid gaat het over een vergoeding voor geleverd werk (lonen), in het geval van kapitaal gaat het over de vergoeding van geleverd (uitgeleend, ter beschikking gesteld) kapitaal (rente, dividend etc). Deze twee delen van het NI noemen we LI (labour income) en CI (capital income).

Dus met andere woorden:

NI = LI + CI

Een inkomen per jaar is een stroom. Het is een stroom geld of goederen die elk jaar weer aan een partij of partijen toevalt. Dus NI, LI en CI zijn stromen.

De hoeveelheid kapitaal in een economie is echter een voorraad. Stel je voor dat je een stroom geld ontvangt en niet alles daarvan opmaakt. Je houdt dan een deel van je stroom inkomen over en legt die apart, op een stapel. Het jaar erop heb je dan weer inkomen maar nu ook een stukje van het jaar ervoor. En zo verder. Dat wat je per saldo opzij hebt gezet (minus interingen en verliezen plus eventuele vergoedingen) noemen we de VOORRAAD kapitaal. Kapitaal is hier losjes gedefiniëerd als de totale voorraad geld, machines, aandelen, spaartegoeden, huizen etc.

Een belangrijke variabele bij Piketty is de verhouding tussen de totale kapitaalvoorraad en het jaarlijkse inkomen. De kapitaalvoorraad noem ik CAP en dan geldt:

beta = CAP / NI

Dus beta is de verhouding (in een land, op enig moment) tussen wat je in een jaar verdient ten opzicht van je totale voorraad kapitaal. Het is een indicatie van je rijkdom: het vertelt hoeveel jaar aan inkomen je op voorraad hebt (hoeveel jaar kun je doorgaan met opmaken als er niets meer bijkomt).

Wereldinkomen per hoofd

We kunnen er nu wat praktische getallen bij zetten om het beeld nog wat duidelijker te maken. In de wereld als geheel hebben we zo’n 7 miljard hoofden/mensen en de totale output van de wereld is ongeveer € 70.000 mrd Euro per jaar. Dat betekent dat op wereldniveau het jaarlijkse inkomen per hoofd van de bevolking ongeveer € 10.000 is. Oftewel ongeveer € 760 per maand.

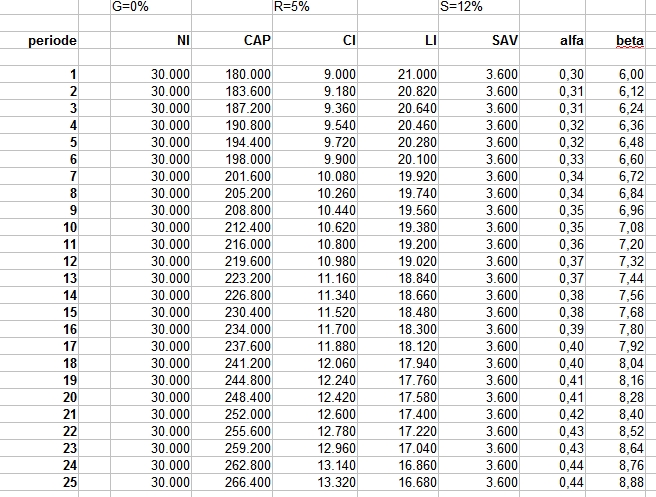
Het gaat hier over een gemiddelde. Er zit een enorme variatie in dat inkomen per jaar per hoofd afhankelijk van waar je in de wereld kijkt. Als we naar het rijkere deel van de wereld kijken (VS, Europa, Japan) dan is dat inkomen per hoofd ongeveer € 30.000 per jaar. Of ongeveer € 2.500 per maand. De hoeveelheid kapitaal is in datzelfde rijkere deel van de wereld ongeveer € 180.000. Ook weer gemiddeld: sommige mensen hebben misschien € 1.000, anderen tientallen miljoenen of zelfs miljarden. Maar gemiddeld dus zo’n € 180.000.

Dat betekent dat de beta in dit geval gelijk is aan 600% (of 6 keer). We hebben dus ongeveer 6 jaarinkomens aan voorraad kapitaal.

CAP = beta . NI = 6 . NI

In de praktijk bestaat die voorraad kapitaal CAP voor ongeveer de helft uit gebouwen en land (zeg maar je huis) en voor de andere helft uit financiëel kapitaal (aandelen, obligaties, banksaldi).

Dus: CAP = € 180.000 = € 90.000 gebouwen + € 90.000 financiëel.

Verdeling naar arbeid en kapitaal

Nu pas kunnen we de stap maken naar het formuleren van de eerste hoofdwet. We zijn namelijk geïnteresseerd in hoe het totale inkomen wordt verdeeld tussen arbeid en kapitaal. We komen er later nog uitgebreider op terug waarom dat interessant is om te weten.

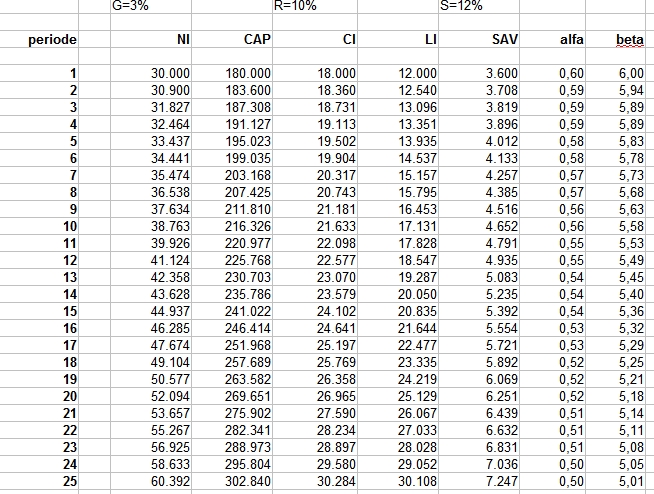
We hebben dan een nieuwe variabele nodig: het rendement op kapitaal, oftewel r. In een andere blog ga ik dieper in op hoe zo’n rendement op kapitaal tot stand komt. Voor nu ga ik uit van het empirische onderzoek van Piketty. Piketty heeft ongeveer 300 jaar data bestudeerd over grote delen van de wereld. Zijn conclusie is dat het rendement op kapitaal gemiddeld zo’n beetje 5% per jaar is. In sommige tijden is het wat hoger, in sommige tijden wat lager. Op enig moment, zelfs als het rendement 5% is, geldt ook nog dat voor risicovolle projecten het rendement wat hoger dan die 5% is (tot 10% of meer) en voor simpele spaarsaldi wat lager (enkele procenten).

Nu kunnen we het aandeel van het NI (totale inkomen) dat naar kapitaal gaat berekenen. We hadden als voorraad CAP € 180.000 en die voorraad krijgt een vergoeding van r = 5%. Dat betekent een stroom aan inkomsten CI van 5% . € 180.000 = € 9.000.

Omdat we al wisten wat het totale inkomen NI was, weten we nu hoe de verdeling van de stroom luidt:

NI = € 30.000 = € 9.000 (CI) + € 21.000 (LI)

Kapitaal krijgt in dit cijfervoorbeeld dus 30% van de totale output en arbeid krijgt de resterende 70% van de output voor het geleverde werk.

De verhouding tussen het kapitaalsdeel (CI) en het totale inkomen (NI) wordt door Piketty ‘alfa’ genoemd.

We kunnen nu de eerste hoofdwet van kapitaal en groei formuleren:

alfa = r . beta

In het cijfervoorbeeld van hierboven betekent dat: 30% = 5% . 6

Je zou kunnen zeggen dat je het aandeel van kapitaal uit de totale jaarlijkse poet kunt berekenen door het rendement (5%) op te blazen met de buffer factor 6.

Rendement

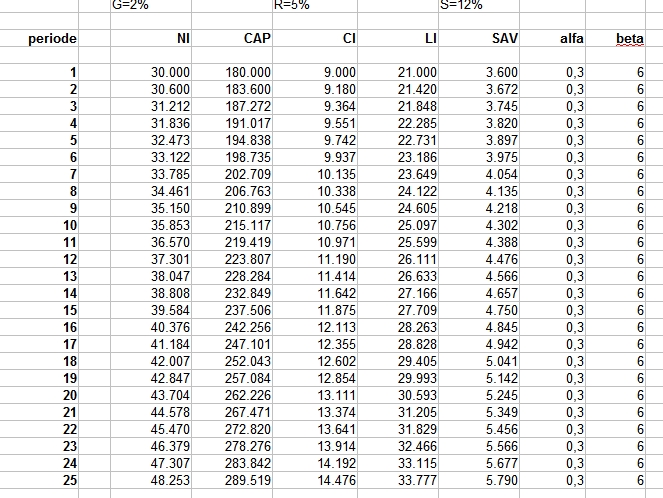
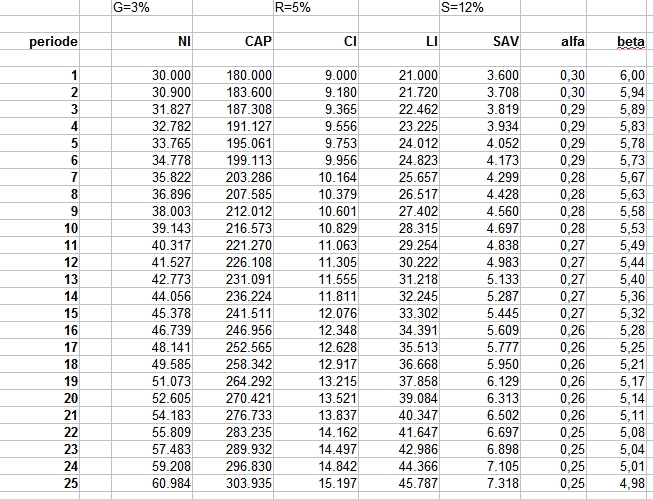
We weten zoals gezegd nog niet waarom r 5% is. Het blijkt uit de cijfers dat het historisch een robuust getal is. De beta is voor ons op dit moment ongeveer 6, maar deze is historisch en over landen minder robuust. Er zijn tijden waarin de beta maar zo’n 2-3 was. Dat betekent dat je maar een paar jaar vooruit kunt met je opgebouwd vermogen. Die situatie geldt/gold bijvoorbeeld voor de periode 1914-1945. In tijden van oorlog (waar veel kapitaal wordt vernietigd en waarbij het jaarlijkse inkomen ook laag is) herkennen we een lagere beta. Ook zien we voor sommige landen in sommige perioden een hogere beta van tegen de 10.

Om beter te snappen hoe de beta tot stand komt moeten we meer weten over de jaarlijkse groei van een economie en over de spaarneiging. Het is de tweede hoofdwet van kapitaal en groei die dieper op deze relatie ingaat. De eerste hoofdwet is vooral een exercitie in boekhouden (wat optellen, aftrekken, delen en vermenigvuldigen). De tweede hoofdwet gaat verder dan boekhouden. Zoetjes aan wordt het interessanter (hoop ik …).

Rudy van Stratum

Systeemdenken (4): De wielrennersparadox (vervolg)

Ik voel me als schaatser en fietser inderdaad onmiddellijk aangesproken door het artikel van Rudy. Eerder kwamen mijn nieuwe schaatsen al eens aan de orde in een artikel over rendement. Nu hebben we het dus over wielrennen. Allereerst, ik ben het grotendeels met Rudy eens, maar het ligt volgens mij wel wat ingewikkelder. Daarover later meer. Eerst een korte anekdote, dan de relatie met slimme financiering, tot slot mijn eigen visie op dit belangrijke onderwerp.

Ik deed een jaar of 5 geleden samen met een vriend mee aan een toertocht door Limburg en de Ardennen, 250 km heuvel op heuvel af. Vanaf 7.00 uur kon je vertrekken en dat deden we dus. Met nog ca. 40 km te gaan kwamen we bij een verzorgingspost een Italiaan tegen. Hij had een gruwelijk oude fiets, een fietsbroek waarvan het kruis op z’n knieën hing en een shirt dat vermoedelijk nog van z’n opa was geweest. Kortom het zag er niet uit. Maar, hij had minstens zo snel gefietst als wij, want eerder vertrekken dan 7.00 uur was niet mogelijk. Hij fietste een aantal kilometers achter ons aan tot hij op de steilste helling van de dag bij ons weg reed. Bij het eindpunt dronken we een biertje, liepen onze Italiaan tegen het lijf en maakten een praatje. Hij werkte sinds een jaar in Nederland, ergens in Limburg en kende daar vrijwel niemand. Wat doe je dan? In zijn geval een beetje fietsen. En als je vrijwel niemand kent heb je daar dus heel veel tijd voor. We hadden het ook over zijn sprint op die steile helling. “Ja, dat komt door mijn oude fiets, ik heb geen lichte versnelling, dus de enige manier om zo’n steile helling op te rijden is door het zo hard mogelijk te doen”. (Gelukkig zei hij daarna dat hij ons op de vlakke stukken bijna niet bij kon houden, dat was aardig van hem. ;-))

Waarmee de kern van Rudy’s verhaal wat mij betreft is bewezen, als je hard wil fietsen, aan je conditie wilt werken of af wil vallen, dan gaat het in eerste instantie niet om het materiaal maar om je inzet. Is dat dan alles en is materiaal dan onbelangrijk? Nee, zeker niet.

Fietsen, systeemdynamiek en slimme financiering
Als ik het artikel van Rudy lees komt bij mij de vraag op, wat had dit ook al weer met slimme financiering te maken? Heel veel wat mij betreft. Net als bij veel andere situaties hebben we hier te maken met één of meerdere doelen en is de vraag hoe je die doelen kunt bereiken. En uiteindelijk kom je dan volgens mij op de vraag hoe je daarbij het hoogste rendement haalt. Zet je doel aan de ene kant als positief (gezondheid, gewicht of wat dan ook), aan de andere kant staan de kosten, geld, blessures, ongelukken, de tijd die het je kost etc. Hoewel tijd, fietsen kan natuurlijk ook gewoon tijdverdrijf zijn, zie het verhaal over onze Italiaan. Meer tijd op de fiets draagt dan bij aan het verhogen van het rendement want het betekent minder verveling en verveling draagt negatief bij.

Waar Rudy volgens mij de mist in gaat is bij de formulering van het doel. Dat is namelijk voor de meeste fietsers niet alleen gezondheid, conditie en een goed gewicht, maar ook ontspanning, buiten zijn, gezelligheid, beetje competitie, je vrienden weer eens zien etc. De een leest een boek, de ander gaat vissen, weer andere gaan naar het café en sommige mensen gaan fietsen. Maar, al deze doelen maken het systeem wel complex. Vooral omdat deze doelen elkaar beïnvloeden. Is het gezellig met je vrienden, dan ga je vaker fietsen en gaat je conditie vooruit. Maar, een goede conditie is ook belangrijk om je vrienden bij te kunnen houden. Als je er steeds afgereden wordt (en er worden later nog grappen over gemaakt ook), dan is er op een gegeven moment weinig meer aan en ga je steeds minder fietsen. Overigens zijn er natuurlijk ook nog heel veel mensen die alleen fietsen.

Een tweede fout die Rudy maakt is te stellen dat het fietsen op een dure nieuwe fiets weinig inspanning vraagt. Zonder me hier verder in te verdiepen en dus gewoon op basis van eigen ervaring durf ik wel te stellen dat die fiets voor niet meer dan 10% de prestatie bepaalt, ik vermoed nog veel minder (dan laat ik het echte oude wrak met aanlopende banden even buiten beschouwing). De andere 90% moet dus gewoon uit het lichaam komen. Nou is 10% beste veel, het kan het verschil zijn tussen je vrienden wel of niet bij kunnen houden. Maar in mijn ogen veel belangrijker aan een fiets is dat die lekker zit, comfortabel, goede versnellingen etc. Een fiets waar je graag op zit en waarop je geen last krijgt van rug, achterwerk, knieën etc. hieronder mijn versie van deze dynamiek, ik heb wat toegevoegd (wijst zich zelf) en enkele woorden veranderd (met rood aangegeven).

Maar stel nu dat je een nieuwe (dure) fiets hebt gekocht, dat was eigenlijk niet nodig want de oude zat ook goed, maar deze is lichter, aerodynamischer en dus sneller. En als je dan geïnvesteerd hebt in deze dure fiets, en je kan nu je vrienden wel bij houden en daardoor ga je nu vaker en verder fietsen en wordt je conditie steeds beter en je gewicht steeds lager, dan is het de investering wel waard geweest. Maar als je net begint met fietsen en nog een buikje weg moet werken, dan is de kans klein dat je opeens je vrienden bij kunt houden. Het is waarschijnlijk beter eerst een jaartje op die oude fiets te trainen, met een mooie beloning (nieuwe fiets) in het vooruitzicht als je je doel gehaald hebt (kilo’s eraf, 5000 km gefietst, noem maar op).

Blijft er één wezenlijk punt over uit het artikel van Rudy, de ratrace om steeds beter materiaal te kopen waarmee je mogelijk sneller zou kunnen gaan. Dient dat nog een doel? Misschien, ergens is er blijkbaar een enorme drijfveer om sneller te kunnen fietsen, vrouwen, aanzien? Er moet iets zijn, op de een of andere manier willen we ons immers steeds weer bewijzen (of in ieder geval is er een groep die dat wil). Helpt steeds beter materiaal daarbij? Niet echt denk ik. Tegenwoordig heb je fietsen die elektronisch schakelen. In plaats van die hendeltjes aan je stuur druk je op een knopje. Lijkt me reuze handig en comfortabel. Maar, was schakelen nou het grote probleem tijdens het fietsen? Nee natuurlijk niet. Het grote probleem is dat de helling te stijl is, de wind te hard waait, je vrienden te snel fietsen en jouw conditie niet goed genoeg is. Het idee alleen al dat iets nieuws zou kunnen leiden tot een hogere snelheid is voor sommige mensen echter alvoldoende om een nieuwe (dure) fiets te kopen. Het rendement van deze investering is twijfelachtig.

Gelukkig zit goed presteren voor een groot deel tussen de oren, als die fiets uit zich zelf al niet sneller is, dan voelt het in ieder geval een stuk lekkerder en sneller.

Stijn van Liefland

Systeemdenken (3): de wielrenners paradox

In eerdere afleveringen over systeemdenken zijn de theezakjes (circulaire economie) en de NS-Prorail discussie (onbedoelde tegenstrevers) aan de orde gekomen. Ditmaal weer een simpel voorbeeld uit het dagelijkse leven, ‘meer theezakjes dan NS’ dus.

Fietsen

Fietsen is hier genomen als voorbeeld. Het had ook kunnen gaan over schaatsen of over hardlopen of over sport in het algemeen. Ik hoop/denk dat de paradox voor veel mensen herkenbaar is.

Het begint vaak bij mannen op een iets gevorderde leeftijd. Een combinatie van ‘een buikje willen wegwerken’ en ‘financieel wat te verhapstukken hebben’. Op een gegeven moment constateer je dan dat je een buikje begint te krijgen en dat je meer aan sport moet gaan doen. Bewegen is goed. Je besluit je oude fiets uit de garage af te stoffen en gaat lekker op de zondagmorgen een uurtje of wat trappen. In het begin valt het niet mee, maar zoetjesaan begin je er toch lol in te krijgen. Je ziet je ‘rondetijden’ verbeteren en praat er ook met collega’s en vrienden over. Voor je het weet rij je mee met een van die clubjes die je op zondagochtend altijd voorbij ziet rijden.

Soms kun je lekker meerijden met het clubje maar soms ook moet je gewoon toegeven dat je het tempo niet bij kan houden. Dat komt natuurlijk omdat die anderen uit dat clubje al langer fietsen. Of omdat ze jonger zijn. Of … omdat ze betere spullen hebben. Jij fietst nog op dat oude ding immers. Omdat je zo lekker bezig bent, vind je dat je jezelf mag belonen met een betere fiets. De techniek staat immers niet stil! Je gaat boekjes lezen, weet inmiddels steeds meer over aerodynamica en veiligheid en energiedrank. Na vele prijsvergelijkingen op internet en het bezoeken van wat specialistische beurzen in het land, stap je naar de dealer om die ene fiets met accessoires te bestellen.

Zo, dat gaat lekker zeg, met die nieuwe fiets. Je raakt nog enthousiaster, je telt weer helemaal mee. Totdat je er na een paar maanden achter komt dat ook met die nieuwe fiets het toch op fysieke inspanning aankomt. En soms kun je toch een zondag niet. Hoe houd ik het ritme vast?

De paradox

De paradox die ik zie is dat het je uiteindelijk om meer beweging en inspanning te doen is. Natuurlijk mag het ook leuk zijn en als je met vrienden fietst geeft dat een sociale verplichting. Allemaal prima. Het basisprincipe is en blijft dat je lichaam inspanning moet leveren. En een oude fiets betekent meer inspanning. Toch is er de escape van een steeds betere en lichtere fiets. Maar dat betekent juist minder inspanning! Bij topsporters die een wereldprestatie willen/moeten neerzetten gaat het om de laatste onsjes en dan is de nieuwste techniek van belang. Dan gaat het om die ene honderste van een seconde sneller. Maar bij onze buikjes-man is dat helemaal niet aan de orde. Soms zie ik zelfs dat de duurste spullen worden aangeschaft nog voordat er serieus is gefietst op wat voor fiets dan ook. Vaak eindigt zo’n actie al na een paar maanden en komt een prima fiets op marktplaats terecht.

In een plaatje

In een systeemplaatje krijg ik dan zoiets:

Ik wil aan beweging gaan doen en ga dus wielrennen. Dat is de cirkel van ‘veel inspanning’. Er is een escape door via betere en vooral duurdere spullen juist minder aan inspanning te gaan doen. Dat is de cirkel van ‘weinig inspanning’. Van Guus hebben we geleerd meer het onderscheid te maken in ‘bovenstroom’ en ‘onderstroom’. Het plaatje hierboven gaat over de bovenstroom, over wat je feitelijk kan zien of constateren. Hij gaat meer wielrennen, hij koopt een betere fiets etc.

Onderstroom

Hoe zou de bijbehorende onderstroom eruit zien? Wat denkt of gelooft deze man-met-buikje? Tja, ik heb daar geen onderzoek naar gedaan maar kan natuurlijk makkelijk de plaats van deze man innemen :-). Ik kom dan tot zoiets:

Ik wil van mijn buikje af. Dat valt nog niet mee. Het ligt niet aan mij maar aan de spullen. Betere spullen is inderdaad fijner maar nog steeds is het niet makkelijk (en het went zo snel). Tja, fietsen is ook maar een manier om af te vallen. Beter is het om gewoon minder te eten. (en nu komt weer een nieuwe dynamiek over eten en duurdere voeding en wel/geen uitzonderingen etc).

Het lijkt er op dat de oplossing centraal komt te staan. In ‘no-time’ gaat het niet meer om het echte probleem (afvallen, gezond leven) maar om de verleidelijke oplossing (je te verliezen in de techniek en het kopen van spullen). Hiermee is de dynamiek dat je het echte probleem uit de weg gaat en vlucht in oppervlakkige en niet-blijvende oplossingen.

Stijn voelt zich als fanatiek schaatser meteen aangesproken en is het hier niet mee eens. Ik zie uit naar zijn versie. Zelf ben ik een audio-nerd en daar ben ik slachtoffer van een soortgelijke valkuil. Ik ga in een andere blog in op deze zogenaamde ‘audio-paradox’.

Rudy van Stratum