Eerder schreven we al over de financieringsconstructie “ons huis verdient het”. Uitgangspunt hierbij is het energieneutraal maken van bestaande woningen door de toekomstige uitgaven aan energie nu te benutten voor investeringen. We hebben de constructie beschreven en aangegeven waar het mis zou kunnen gaan. Voor een samenvatting kijk naar de twee infographics die we toen gemaakt hebben. Nu zijn we via via op een initiatief gestuit dat gezamenlijk energiemaatregelen probeert in te voeren in Amsterdamse woningen. Ik wil dat met de bril van tegendenken analyseren. Het is een nogal lang verhaal geworden, daarom hier eerst even een korte inhoudsopgave:
- Waarom tegendenken?
- Kanttekeningen bij uitspraken, kritisch op de feiten
- Doorrekenen
- Conclusie en wat dan wel?
Waarom tegendenken?
Wij vinden investeringen in energiebesparing en duurzame energie belangrijk. Argumenten zijn er voldoende. Tegengaan van klimaatverandering, minder afhankelijk van het buitenland, financieel aantrekkelijk, tegengaan van uitputting van hulpbronnen, minder milieuvervuiling, etc. Soms heb ik ook wel eens twijfel bij een argument, maar het gehele pakket geeft meer dan genoeg motivatie om achter dit soort investeringen te staan.
Een belangrijke uitdaging is mensen te laten investeren in de eigen woning. Om dit voor elkaar te krijgen moeten we met een goed verhaal komen. Een verhaal dat enerzijds gaat over milieu, toekomst, grondstoffen etc. en anderzijds over de financiële kant. Het moet een verhaal zijn waarvan mensen (1) intuïtief aanvoelen dat het klopt en (2) bij het doorrekenen de bevestiging zien. Het eerste is belangrijk om mensen aan het denken te krijgen, te zorgen dat ze serieus overwegen dit soort maatregelen te nemen. Het tweede is belangrijk om ze definitief over de brug te krijgen. Maar, het tweede is ook belangrijk voor de geloofwaardigheid van dit soort projecten.
Om dat laatste is het mij te doen, als we serieus werk willen maken van energieprojecten moeten we er voor zorgen dat we onze geloofwaardigheid behouden. Dat betekent dat je kritisch moet zijn, de risico’s en onzekerheden serieus moet nemen, de juiste argumenten moet gebruiken en eerlijk moet zijn. Tegendenken dus waarbij de site www.weterringduurzaam.nu als voorbeeld dient, maar ze zijn niet de enige, er zijn veel vergelijkbare initiatieven in Nederland.
Uitspraken en feiten
Hier een aantal uitspraken en cijfers die gebruikt worden om mensen aan te sporen tot investeringen. Ik haal een aantal uitspraken van de site en plaats daar kritische kanttekeningen bij. Ter info, alle cursief gemaakte tekst komt van de site.
Energieprijzen stijgen met 5%
“…een gemiddeld huishouden geeft volgens het Nibud per maand €96 euro aan gas en € 55 aan electriciteit uit. Per jaar is dat totaal €1812. Berekend over de komende 15 jaar en rekening houdend met een stijging van de energieprijs voor kleinverbruikers (de gewone huishoudens) van 5 %, is dat totaal meer dan € 41.000 ! Stel dat u dat bedrag besteedt aan energiemaatregelen aan uw huis, dat het wooncomfort verbetert en dat die maatregelen zichzelf terugverdienen binnen 15 jaar? Dan heeft u bij niets doen over 15 jaar ‘alleen’ maar € 41,000 aan het energiebedrijf gegeven. En uw huis is nog even ‘lek’ als nu. Terwijl nieuwbouw huizen over 15 jaar al lang energieneutraal zijn. “
Op de 15 jaar en de € 41.000 kom ik aan het einde terug als we gaan rekenen. In eerste instantie val ik over de 5% stijging van de energieprijzen. Ik vind dat erg hoog en zou daar niet van uitgaan als ik zelf een investering zou doen. Het is een heel gezoek, maar uiteindelijk heb ik op de site van het CBS dan toch een reeks met gasprijzen en elektriciteitsprijzen over de afgelopen 20 jaar gevonden.
En ja, het blijkt te kloppen, de afgelopen 20 jaar zijn de prijzen inderdaad met ca. 5% per jaar gestegen. Als feit klopt het dus, maar ik wil er wel een aantal kanttekeningen bij plaatsen. Er was ook sprake van inflatie (gemiddeld ca. 2%), daar houdt mijn reeks voor zover ik kan nagaan geen rekening mee, relatief is de stijging dus lager. Een tweede punt is dat de prijsstijging grillig is. Soms stijgt de prijs in een jaar met meer dan 10%, andere jaren is er sprake van een daling. Een derde punt is dat de prijzen de afgelopen 7 jaar niet gestegen zijn. Conclusie, feitelijk klopt het, maar het is riskant deze 5% als uitgangspunt te nemen. Beter is een aantal scenario’s te nemen.
Een energiezuinig huis is meer waard
“Een energiezuinig huis is bovendien meer waard dan een vergelijkbaar energieslurpend huis.”
Ik kan daar niets tegenin brengen. De site geeft zelf al aan dat nog moet blijken hoeveel de waarde stijgt. Maar belangrijker, van alleen waarde kun je niets kopen. Zolang je je huis niet verkoopt heb je niets aan deze extra waarde. De bewoners zelf hebben natuurlijk wel degelijk iets aan deze waarde, namelijk meer comfort. Als je echter 5 jaar na je investering een boot wilt kopen, dan leidt deze extra waarde niet tot een boot. Sterker nog, een hogere waarde van een huis zou tot een hogere OZB aanslag kunnen leiden. In dit stuk legt Rudy het verschil tussen prijs en waarde uit. Nog even verder met de waardestijging.
“De TiasNimbas Business School in Tilburg meet sinds de invoering ervan in 2008 vier keer per jaar het effect van het energielabel op de marktwaarde van woningen. Uit de metingen blijkt dat woningen met een energielabel sneller verkocht worden, en dat woningen met een ‘groen label’ gemiddeld 4 % meer opbrengen dan vergelijkbare woningen die niet energiezuinig zijn.”
Het gaat om een investering van ruim € 41.000, maar voor het gemak ga ik uit van € 40.000. Door de oogharen kijkend zie je zo dat de investering zich niet terugverdient bij de verkoop van de woning. De € 40.000 investering is gebaseerd op een gemiddelde woning, maar laten we voor het gemak een woning van € 400.000 nemen die we voor € 40.000 energieneutraal kunnen maken, we hebben het dan over een investering van 10% van de waarde van de woning waardoor de woning 4% meer waard wordt. En, dat dan ook nog bij een zeer gunstig scenario, een woning die veel duurder is dan gemiddeld met een investering die veel lager is dan gemiddeld. Totale kosten woning € 440000 (4000.000 + 40.000 maatregelen), verkoop voor € 416.000 (400.000 + 4%).
Stel vakantie of aankopen uit
“Ja het lijkt me een goed idee maar daar heb ik nu even geen geld voor”. Een voor de hand liggende eerste reactie. Maar overweeg de mogelijkheid eens om iets anders niet te doen. Bijvoorbeeld door uitgaven die zichzelf niet terugbetalen uit te stellen: een keer niet op vakantie gaan en in plaats daarvan aan de slag met je huis levert vanaf dat moment jaarlijks een besparing op… die voortaan wellicht aan de vakantie, of iets anders, besteed kan worden.”
Op zich klopt dit natuurlijk, we hebben het dan wel over een hele dure vakantie. Maar laten we een auto nemen die voor het gemak ook precies € 41.000 kost. Je kunt natuurlijk geen auto nemen en gebruik maken van OV of greenwheels en de € 41.000 in de woning stoppen. Echter, dat is niet wat gesuggereerd wordt, het idee is hier het uitstellen van de aanschaf. Maar voor hoe lang? Na een jaar of 5 zal die auto er toch een keer moeten komen, dan heeft de investering zich nog lang niet terugverdient en is het geld er dus niet.
Belangrijker is echter dat hier volgens mij een fout van een hele andere orde gemaakt wordt. De initiatiefnemers verplaatsen zich hier te weinig in de huiseigenaren. Ik geloof niet dat er iemand is die een keer niet op vakantie gaat om energiemaatregelen te nemen. Ja vooruit, als energiebesparing je hobby is of als je een huis hebt dat zeer oncomfortabel is. Je vakantie stel je uit als je het geld echt nodig hebt, als de auto, de wasmachine en CV tegelijkertijd kapot gaan of als het dak van je huis dreigt af te waaien.
Spaarrente
“Er wordt beweerd dat investeren in energiemaatregelen momenteel meer oplevert dan geld op de bank laten staan. De spaarrente is immers historisch laag en de energieprijzen blijven maar stijgen. Dat zou betekenen dat het een goed idee is om niet af te wachten maar snel aan de slag te gaan en om zo snel mogelijk te kunnen ‘oogsten’.”
Ik vind dit wel mooi. De energieprijzen blijven maar stijgen terwijl de spaarrente historisch laag is. Over de energieprijzen hebben we het al gehad, historisch klopt een stijging van 5% maar dat ze maar blijven stijgen is onzin. In de toekomst is een stijging goed mogelijk, maar de afgelopen jaren was dit niet het geval. Dan de spaarrente, die is historisch laag en impliciet wordt hier de verwachting uitgesproken dat dat ook de komende jaren zo zal blijven. Het is me niet gelukt een goede reeks met rentetarieven van de afgelopen jaren te vinden. Maar, als ik in mijn oude boekhoudingen kijk kom ik in 2008/9 spaarrentes tegen van 3,75 tot 4,75% op hele normale spaarrekeningen, zonder allerlei beperkingen. Wellicht is de rente nu historisch laag is, het betekent ook dat de kans dus erg groot is dat de rente weer gaat stijgen. Of anders gezegd, dan is de kans toch klein dat de rente 15 jaar lang historisch laag blijft.
Rekenen
Investeren met eigen geld
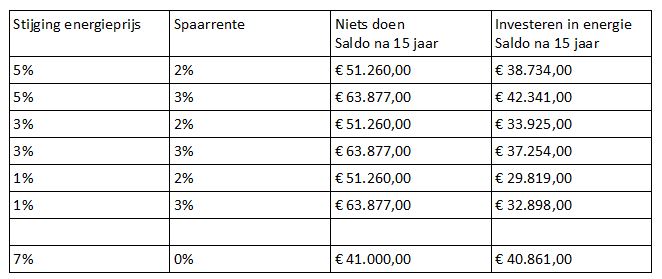
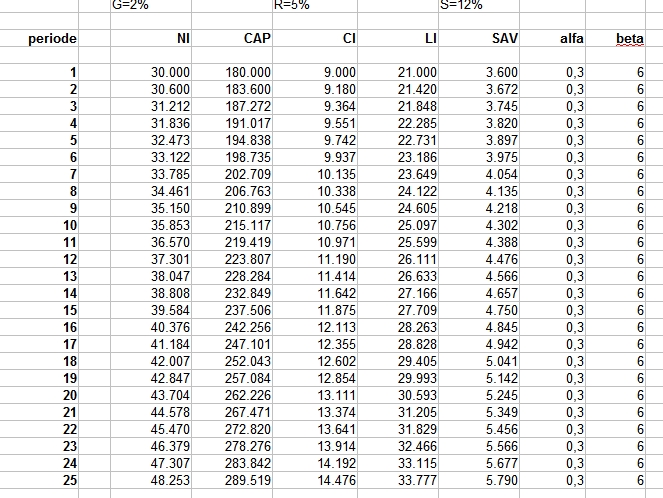
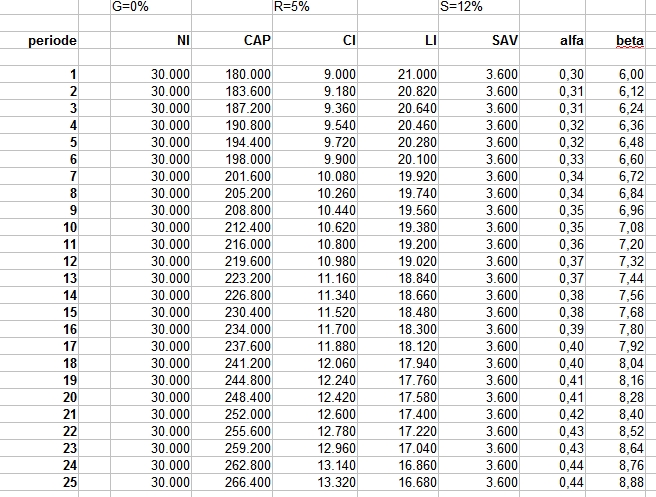
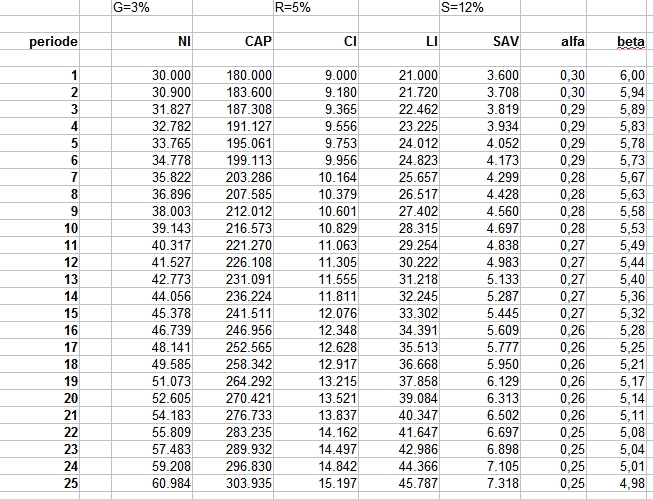
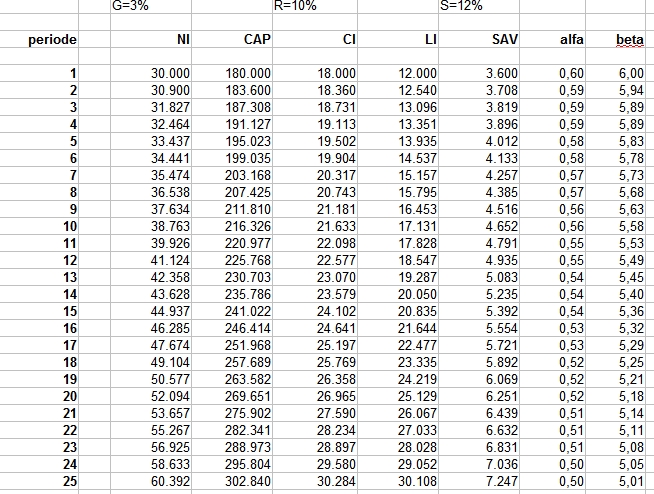
In dit geval betekent tegendenken ook nog alles even narekenen. Ik heb alle cijfers in een spreadsheet gezet, investering 41.000, uitgaven aan energie in het eerste jaar € 1.812,=. Dan zijn er twee belangrijke variabelen, de spaarrente en de stijging van de energiekosten. Onderstaande tabel geeft de resultaten voor een aantal scenario’s. In de eerste twee kolommen de twee variabelen, in de laatste twee kolommen het saldo op de bank. Uitgangspunt hierbij is dat in jaar nul 41.000 beschikbaar is waarbij je de keuze hebt dit op de bank te laten staan (derde kolom) of te investeren in maatregelen. Elk jaar is er dan een bepaald bedrag (de energierekening) dat je ofwel betaald aan het energiebedrijf (niets doen) ofwel op een spaarrekening zet waar je dan vervolgens rente over krijgt.
Snelle conclusie, we geven per jaar domweg te weinig uit aan energie om een investering van € 41.000 financieel te verantwoorden. Alleen bij een hele lage rente en een enorme stijging in energieprijzen is dit te verantwoorden (zie onderste regel). Natuurlijk kunnen ook subsidies helpen. Om het compleet te maken, bij het scenario 3% stijging van de energieprijzen en 3% rente duurt het 25 jaar voordat beide scenario’s tot eenzelfde banksaldo komen. Overigens hebben we onderhoudskosten en vervangingskosten allemaal niet meegenomen, we gaan er maar van uit dat die gelijk zijn als bij niets doen.
Investeren met geleend geld
Tot slot in dit blokje rekenen even terug naar onze eerdere artikelen en infographics. Daar was het uitgangspunt dat het geld geleend zou worden. Hoe zien de cijfers er dan uit?
Blijkbaar was er geen geld voor de investering, dus het scenario niets doen begint in dit geval met een saldo van € 0,= op de bank en ongeacht de rente zal dat altijd € 0,= blijven. Ook voor het scenario wel investeren geldt: er is geen geld beschikbaar, dus rente en aflossing moeten gefinancierd worden uit het bedrag dat anders aan het energiebedrijf zou worden betaald. Als er in een jaar meer geld wordt uitgespaard dan aan rente wordt betaald, dan wordt dat gebruikt voor het aflossen van de lening. Als de rente op een lening bijvoorbeeld 4% bedraagt dan betaal je in het eerste jaar de lening € 1.640,= terwijl je € 1812 uitspaart aan energielasten, het verschil van € 172,- gebruik je om een deel van de lening mee af te lossen. Allemaal theorie, in de praktijk loopt dit natuurlijk anders, maar voldoende om te kunnen zien wat er gebeurt.
Ook hier kunnen we weer eindeloos varièren met de rentetarieven. Ik zie drie mogelijkheden:
- Aanvullende hypotheek, met hypotheekrenteaftrek, ca 2% netto rente
- Aanvullende hypotheek, zonder hypotheekrenteaftrek, ca 3% rente
- persoonlijke lening bij een bank, ca. 5% rente
De stijging van de energielasten heb ik op 5% en 4% gesteld. Daar kan je nog veel meer in variëren, maar dat heeft allemaal weinig zin. Het duurt gewoon lang voordat je zo’n lening hebt terugbetaald.

Conclusie en wat dan wel?
De belangrijkste conclusie, als je per jaar € 1.812 aan energie betaalt dan is het financieel niet slim om € 41.000 te investeren in besparende maatregelen. Je verdient het geld wel terug, maar het geld gewoon op de bank laten staan levert meer op. Dit geldt ook voor een lening, uiteindelijk is die te financieren vanuit de mindere energielasten, maar de looptijd wordt erg lang en daarmee ook de risico’s voor de financier en daarmee de rente. Dat hebben we allemaal niet meegenomen. De waardestijging van de woning zet ook weinig zoden aan de dijk.
Wat dan wel?
- Ten eerste gaat het natuurlijk niet alleen om financieel rendement. Er zijn mensen die het geld gewoon hebben en er niets mee doen (een erfenis, loterij, gewoon zuinig geweest etc.) en het goed kunnen missen. Dan is het prima om dit soort investeringen te doen. Het levert wellicht niet het hoogste rendement maar heel slecht is het nou ook weer niet en het levert een betere woning op. Dus als het je niet om financieel rendement gaat, kun je dit gerust doen.
- Als tweede zou ik er voor kiezen een aantal maatregelen uit te kiezen die tot energiebesparing of duurzame energie leiden en wél financieel rendement hebben. Het laaghangende fruit plukken dus. Om een woning energieneutraal te krijgen is veel geld nodig, veel minder is er nodig als je niet tot het uiterste gaat. Voor welk bedrag kan je een woning “75% energieneutraal” maken? Stel nou dat je die € 41.000 hebt, kunt missen en in energie wilt investeren. Dan is het lucratiever om voor dat bedrag je eigen woning en dat van de buren aan te pakken en daar zo veel mogelijk rendabele maatregelen te nemen dan je eigen woning voor 100% aan te pakken. Je moet natuurlijk wel een goede regeling met de buren in elkaar draaien.
- Ten derde, vertel het eerlijke verhaal en vergeet daarbij niet ook de risico’s en onzekerheden een plek te geven.
Stijn van Liefland