Even wat spelen met de cijfers. We gaan uit van de basissituatie zoals door Piketty genoemd. Ik verwijs naar de eerdere blogs over de 2 hoofdwetten.

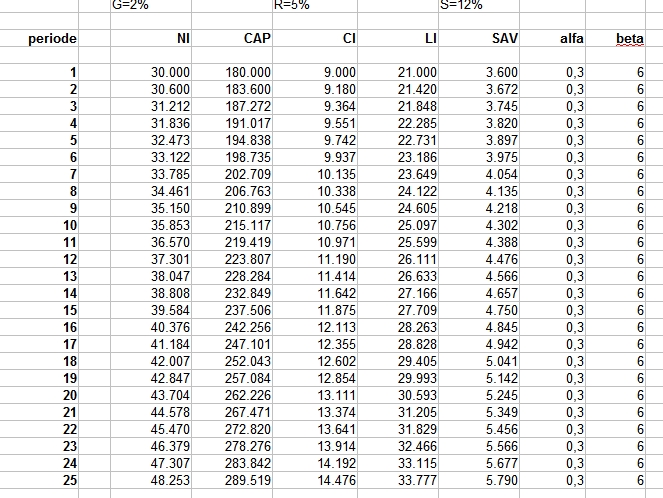
Het nationale inkomen NI = 30.000 per jaar. De kapitaalgoederenvoorraad CAP = 180.000 per jaar. De vergoeding op kapitaal R=5%. Het groeipercentage van de economie G=2%. Het spaarpercentage S=12%. Beta geeft de kapitaal-inkomensverhouding weer, door Picketty in 2010 op ongeveer 6 ingeschat. Alfa geeft het aandeel van kapitaal in het nationaal inkomen weer en is gesteld op 30%.

Het basisscenario

Hier zie je mooi dat bij een groei van 2% van de economie alle verhoudingen netjes constant blijven.

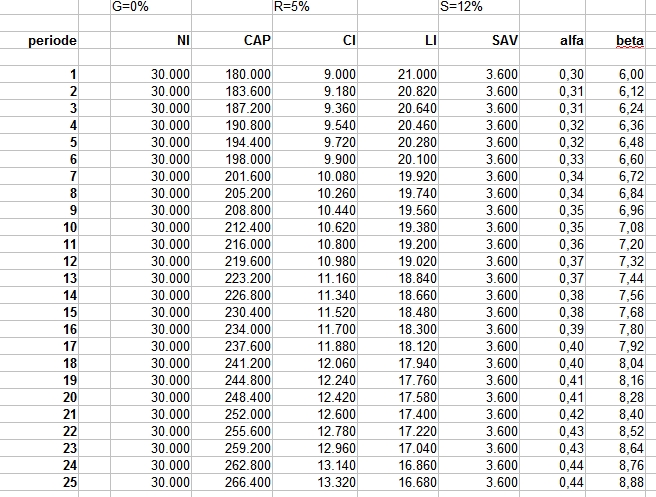
Een groei van 0%

Benieuwd wat er gebeurt als de groei tot stilstand komt?

Nu zie je inderdaad dat het kapitaalsaandeel in de economie steeds groter wordt. Er blijft op termijn niets meer over voor beloning voor arbeid. Deze situatie is zelfs instabiel omdat er geen einde zit aan de hoogte van beta (delen door 0 mag niet!) en uiteindelijk zou LI zelfs negatief worden (wat in dit modelletje niet is toegestaan natuurlijk). Maar het idee is duidelijk: een zekere groei van de economie is nodig om tegenwicht te bieden aan de rentevergoedingen op kapitaal.

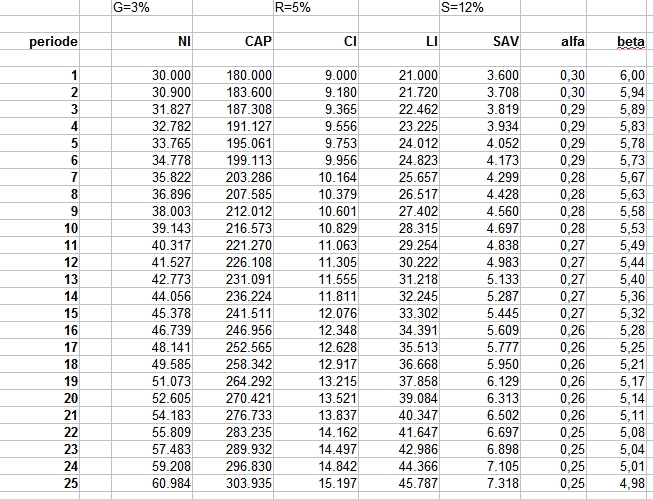
Een groei van 3%

Wat gebeurt er als we aannemen dat de economie wat sneller groeit (maar minder snel dan het rentepercentage)?

Nu kun je zien dat bij een groei van 3% het kapitaalsaandeel zal dalen. En dat ondanks dat de vergoeding op kapitaal R=5%. Volgens de formule/hoofdwet beta = s / g zal beta verder blijven dalen en langzaam naar de waarde van 4,00 gaan. De alfa gaat langzaam naar de waarde van 0,20. Je ziet hier het bewijs dat r > g geen probleem hoeft te zijn. Alleen mag het verschil tussen r en g niet te groot worden (in deze rekenvoorbeeldjes mag de groei van de economie dus niet meer dan 3%-punten onder de vergoeding op kapitaal liggen).

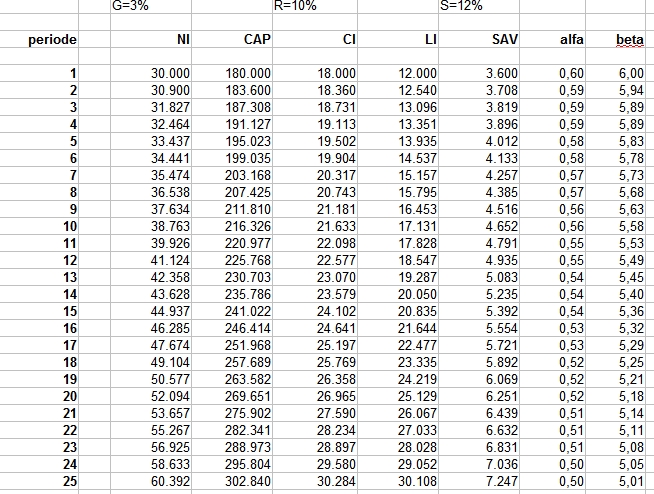
Rente omhoog

Met hoeveel moet de rente dan stijgen om bij een hogere groei van 3% toch weer een beta van 6 te krijgen? Nou, dat gaat dus niet lukken. Ik heb een hele hoge rente genomen van 10%. De beta zal op termijn toch weer gewoon naar de waarde 4 gaan (s/g namelijk, die is niet afhankelijk van r). Maar de alfa zal op termijn hoger eindigen (start ook flink hoger) op een waarde van 0,40 (namelijk r x beta).

Genoeg gepield met de formules en getallen van Picketty. Hopelijk is er zo wat gevoel ontstaan bij de logica achter de hoofdwetten. Probleem blijft dat dit rekenmodel een aantal zaken fixeert (exogeen veronderstelt) die eigenlijk zelf ook weer verklaard moeten worden. Als we dat ook gaan uitwerken (wat op zich prima kan) dan krijgen we een compleet economisch model en verlaten we de bespreking van Picketty. Toch ga ik in de volgende blog in woorden (zonder formules) wel in op de mogelijke verbanden.

Rudy van Stratum

 

Voor de liefhebbers hier het totale rekenmodelletje met de 2 hoofdwetten:

(1) NI = NI(-1) . (1+g)

(2) SAV = s. NI

(3) CAP = CAP(-1) + SAV

(4) CI = r . CAP

(5) LI = NI – CI

(6) alfa = CI / NI ( via substitutie van (4) en (7) in (6) volgt dat alfa = r . beta, hetgeen de 1e hoofdwet vormt)

(7) beta = CAP / NI

De tweede hoofdwet (beta = s / g) heb ik noch Picketty in zijn boek afgeleid (wat lastiger!) en geldt niet altijd op elk moment en wordt in de simulaties hierboven wel duidelijk zichtbaar op de langere termjin.