Tag archieven: rendement

Rendement (3), tijdsaspect en alternatieve scenario’s

We sloten de tweede aflevering af met de opmerking dat € 100,= nu meer waard is dan € 100,= over 4 jaar. Stel ik krijg elk jaar 2% rente op mijn spaarrekening, dan is € 100,= nu over 4 jaar € 108,=, zelfs een beetje meer als je rente over rente meeneemt. Hoe nemen we dit nou mee als we het hebben over een investering? Er zijn allerlei methoden waarmee je bedragen in de tijd kunt vergelijken zoals de “netto contante waarde” en “eindwaarde”. Wij gaan dit soort begrippen hier niet verder uitleggen, er zijn genoeg sites die dat doen en er is voldoende literatuur over. Hier gaan we in op de vraag wat tijd en geld en rendement met elkaar te maken hebben, tot welke overwegingen dit leidt en wat voor consequenties die heeft voor investeringsbeslissingen.

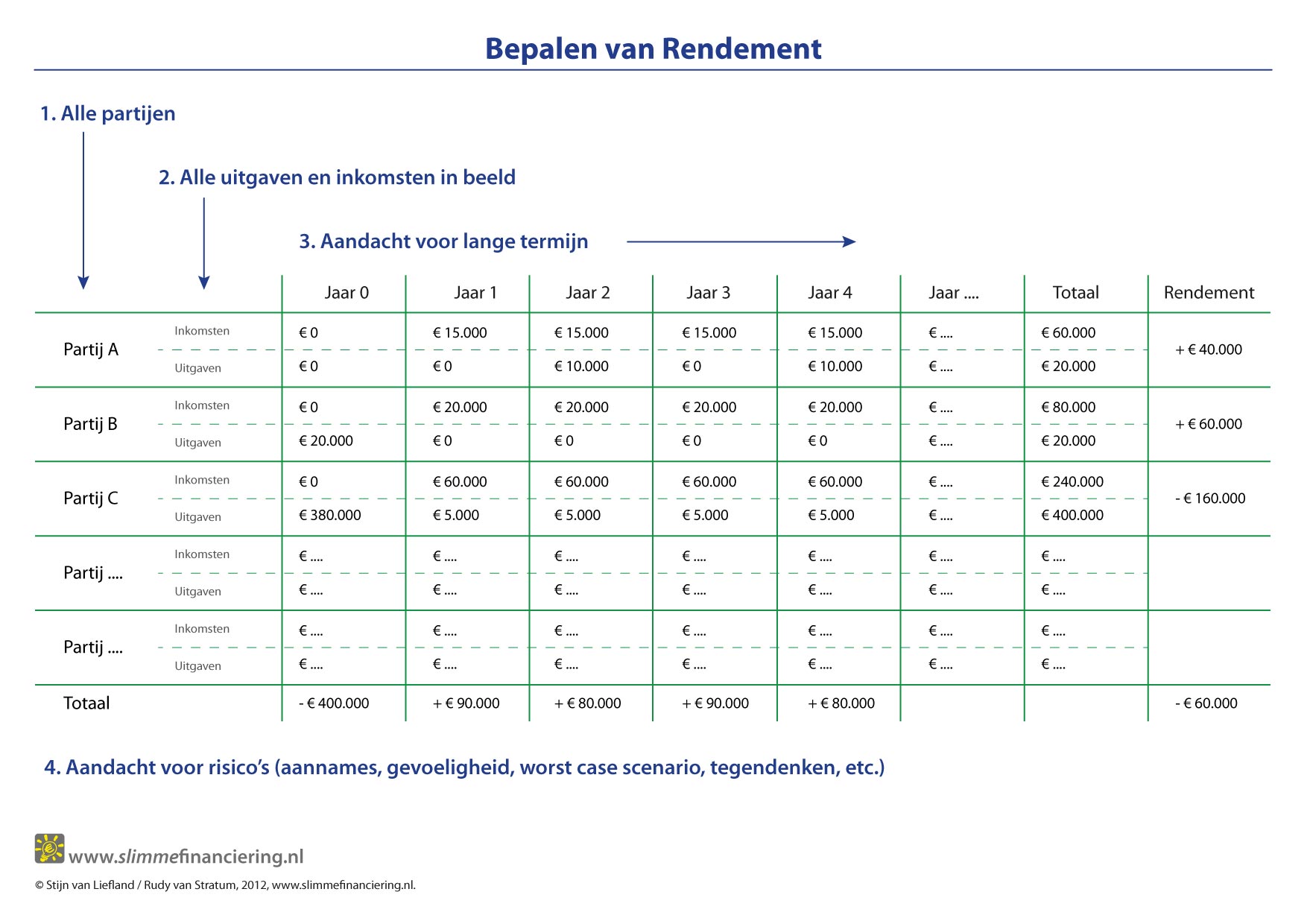
We hebben weer een voorbeeld van een investering van in totaal € 4.500, verdeeld over drie partijen met een looptijd van 5 jaar. Zo op het eerste gezicht leidt deze investering over een periode van 5 jaar tot een verlies van € 750,= over de drie partijen, financieel gezien geen verstandige investering.

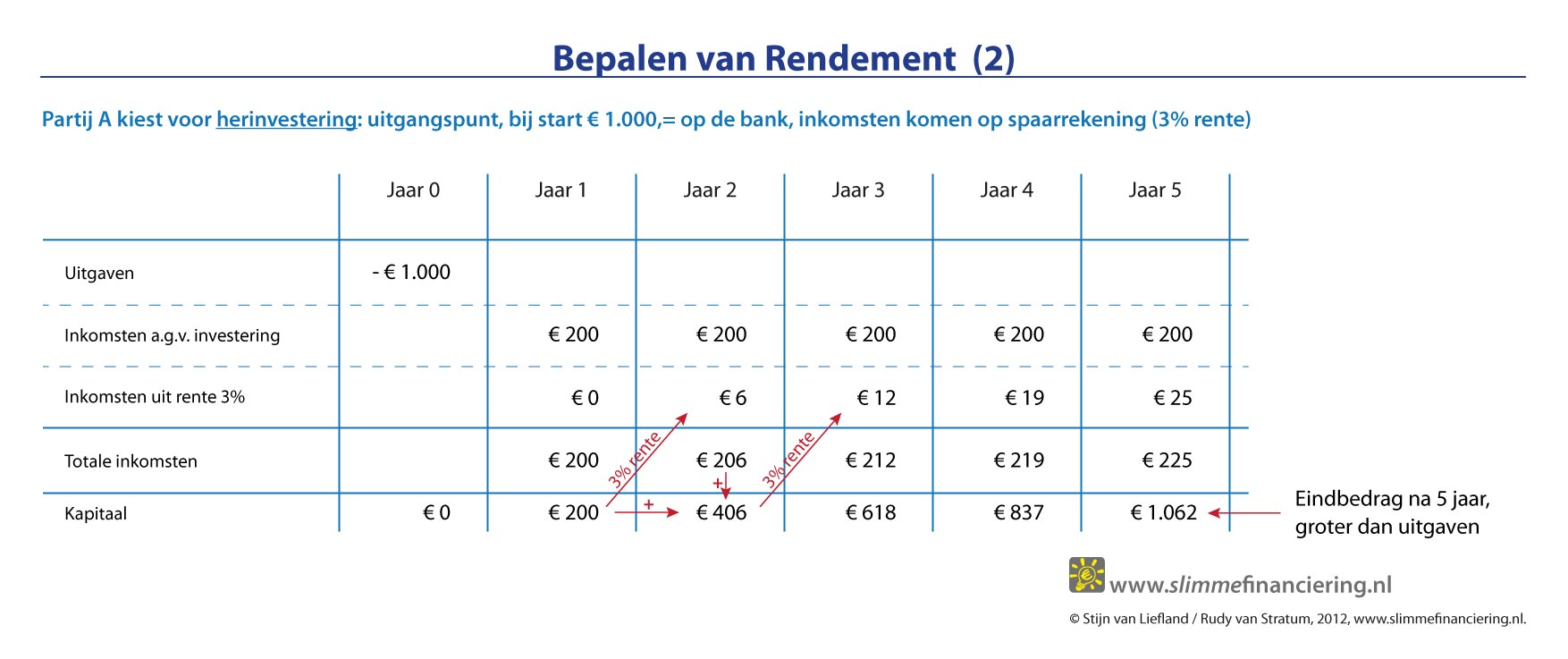
Herinvesteren

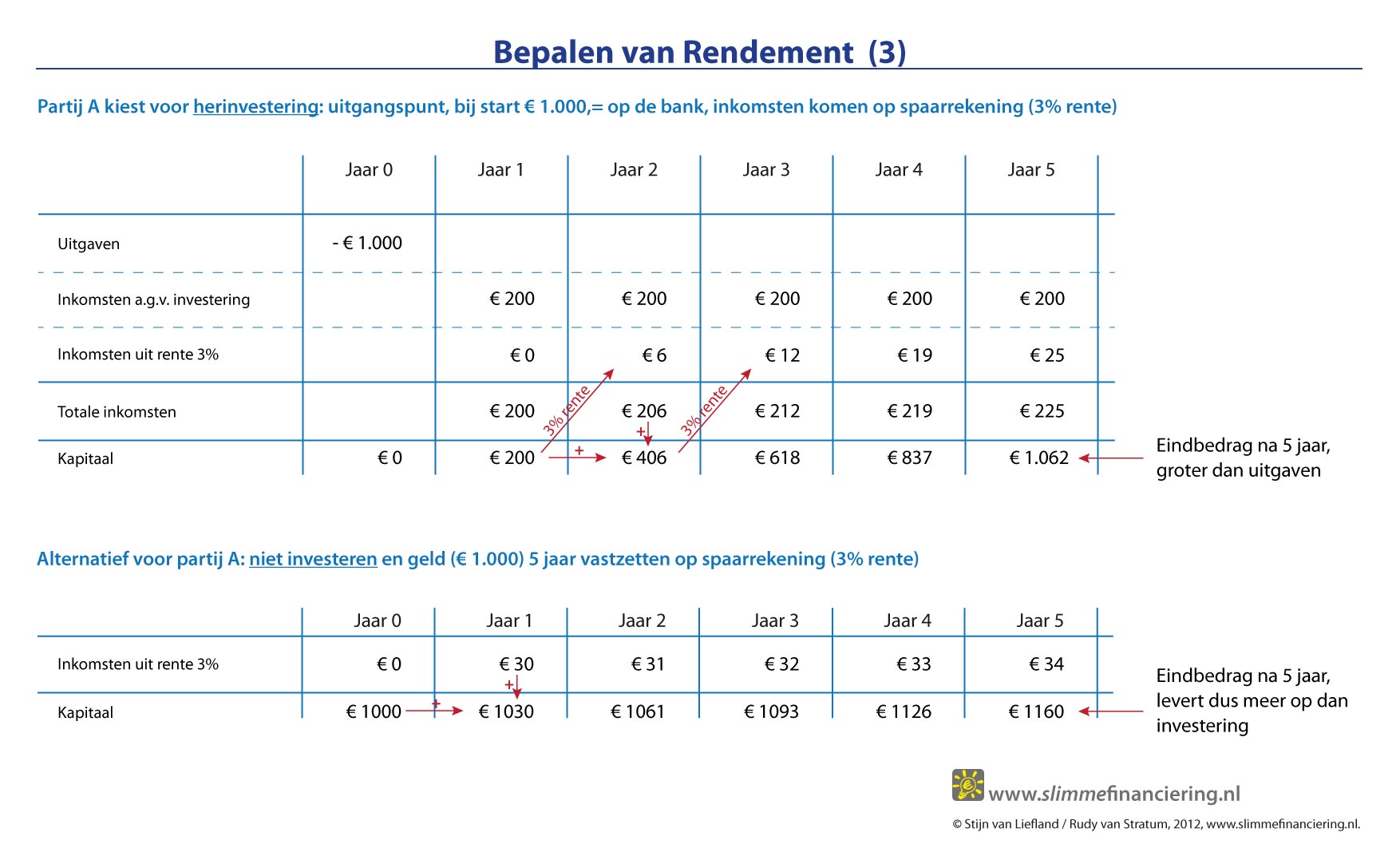
We focussen nu op partij A, deze investeert € 1000,= en de inkomsten bedragen € 200,= per jaar. Na vijf jaar heeft partij A de investering terugverdient (in jaar 0 had partij A € 1.000 op de bank, aan het eind van jaar 5 ook). Partij A heeft echter de optie om het geld dat jaarlijks binnenkomt weer op de bank te zetten of ergens anders te investeren. Als partij A voor de bank kiest ontvangt A elk jaar rente over inkomsten van de jaren daarvoor. Onderstaande figuur laat dit zien, de inkomsten uit jaar 1 (€ 200,=) leveren aan het eind van jaar 2 € 6,= rente op (uitgaande van 3% rente). Aan het eind van jaar 3 ontvang A de gebruikelijke inkomsten (€ 200,=) en rente over het kapitaal dat op de bank staat, inmiddels gegroeid tot € 406,= (€ 200 uit jaar 1, € 200 uit jaar 2 en aan het eind van jaar 2 3% rente over de € 200 uit jaar 1 die het hele jaar 2 op de bank heeft gestaan). Als we zo de hele periode van 5 jaar doorrekenen komen we op een bedrag van € 1.062,=. De investering blijkt voor partij A een stuk gunstiger te zijn dan we aanvankelijk dachten, er wordt in 5 jaar € 62,= verdient.

Alternatieven rendement

Maar, dit verhaal met rente heeft ook een andere kant. We moeten nu ook kijken wat er gebeurt als A besluit om helemaal niets te doen. Figuur laat zien wat er gebeurt als A besluit niet te investeren en het geld gewoon op de bank te zetten tegen een rente van 3%. Na vijf jaar heeft partij A dan € 1.160,=, bijna € 100,= meer dan in het geval A investeert in ons project. Als partij A op basis van financiële argumenten een keuze maakt is duidelijk hoe deze uitpakt.

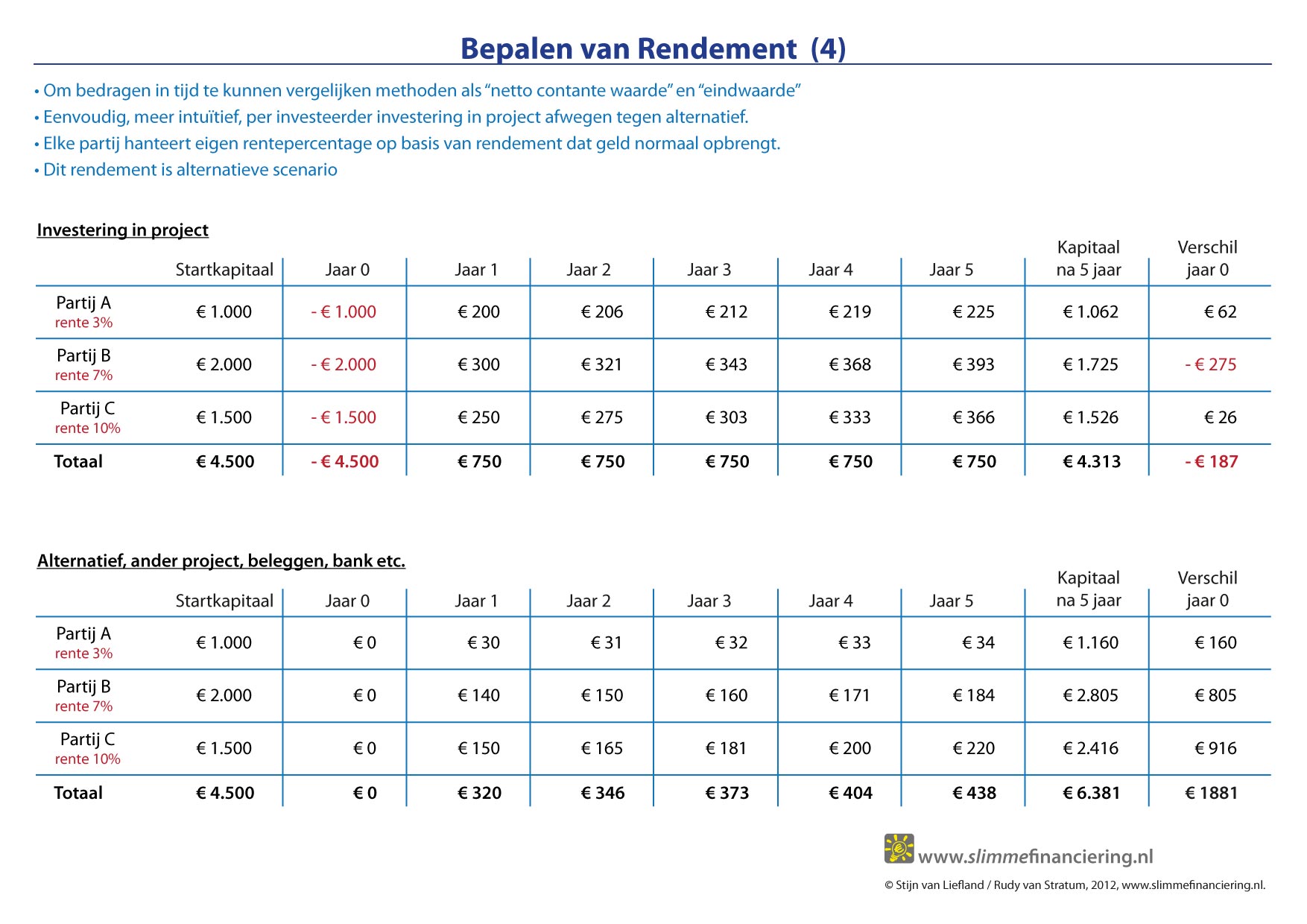
We kunnen dit ook voor alle andere partijen uitrekenen. Onderstaande figuur geeft een overzicht weer voor alle drie de partijen waarbij ze de inkomsten weer opnieuw investeren. Daarnaast is voor elke partij uitgerekend wat een alternatief scenario oplevert. Hierbij is voor elke partij een andere rentepercentage gehanteerd (daarover later meer). Duidelijk is dat het alternatieve scenario de partijen veel meer oplevert dan investeren in een gemeenschappelijk project. Eén ding hebben we daarbij niet meegenomen, de gevolgen van de keuze voor het alternatieve scenario. Het zou natuurlijk kunnen dat één van de partijen extra uitgaven heeft als dit project niet doorgaat. Denk aan schade die kan ontstaan door iets niet te doen of een boete die we moeten betalen als we bepaalde maatregelen aan milieu of natuur niet uitvoeren. Deze kosten moeten we uiteraard ook meenemen en komen als jaarlijkse (of eenmalige) kosten in het overzicht dat we maken over alle partijen.

Zoals gezegd hebben we voor alle partijen een andere rentepercentage gehanteerd. Dit percentage zegt iets over het rendement dat de partij normaal gesproken over haar geld maakt, of in ieder geval wil maken. Voor de ene partij is dat rendement niet zo belangrijk (overheid, non profit) voor andere wel. Het is belangrijk dit vooraf in beeld te hebben. Een ondernemer mee laten betalen aan een investering die een rendement van 8% oplevert lijkt heel aantrekkelijk. Maar, als die ondernemer weet dat er ook investeringsmogelijkheden zijn met een rendement van 10% (bijvoorbeeld personeel vervangen door een machine) dan is 8% financieel gezien minder aantrekkelijk.

Conclusies rendement

Op de een of andere manier moeten we bij het bepalen van rendement rekening houden met de tijd, geld nu is meer waard dan geld over een aantal jaar. Een eenvoudige manier is de investering te vergelijken met een alternatief.
Als we ons voorstel vergelijken met een alternatief scenario moeten we ook de kosten meenemen die we moeten maken als ons project niet doorgaat (bijvoorbeeld schade of een boete).
Wat een voldoende rendement is bepaalt elke partij zelf, op basis van alternatieven en rendement dat in het verleden gehaald werd.

Rendement (2), meerdere partijen

In de vorige aflevering hebben we naar rendement gekeken bij één partij met een relatief simpele ingreep. In de praktijk zijn wij vaak betrokken bij projecten waar meerdere partijen investeren en meerdere partijen als gevolg van die investering inkomsten hebben. Het komt dan vaak voor dat de inkomsten en uitgaven niet gelijk over partijen verdeeld zijn, de ene partij geeft vooral uit, een andere partij verdient (het bekende probleem van de woningbouwcorporatie die woningen gaat isoleren). Hoe gaan we hier met rendement om?

In de kern is het in zo’n geval niet veel anders dan bij ons eenvoudige voorbeeld. Beschouw alle partijen gezamenlijk als één partij en kijk wat over alle partijen, door de tijd, de inkomsten en de uitgaven zijn. Als er over alle partijen meer geld binnenkomt dan uitgegeven wordt dan is er sprake van een positief rendement. Onderstaande figuur laat dat voor een fictieve casus overzichtelijk zien (klik voor vergroting).

Er zijn in dit geval drie partijen bij dit project betrokken. In jaar nul wordt een investering gedaan, de jaren daarna zijn er inkomsten maar ook uitgaven voor onderhoud. Voor elke partij zijn de jaarlijkse inkomsten en uitgaven opgenomen, per partij kunnen we na een bepaalde periode (hier vier jaar) een rendement berekenen (eigenlijk geen rendement maar resultaat). Als we dat allemaal optellen komen we rechts onderin tot een totaal, in dit geval – € 60.000. We hebben dus een negatief resultaat over alle partijen, het advies zou dan ook zijn dit niet te doen. De gezamenlijke partijen worden hier financieel niet beter van. Je kunt lang of kort praten over het herverdelen van uitgaven of inkomsten, je komt er niet uit zolang er sprake is van een negatief rendement. Het enige dat je met elkaar kunt verdelen is het verlies.

Anders is het als er rechts onderaan een positief bedrag uitkomt (stel € 40.000). Dan is er wel wat te verdelen. Als alle aannames kloppen dan is er na vier jaar € 40.000 over de drie partijen te verdelen. Doen we de investering niet, dan is er niets te verdelen. Het kan dus niet zo ingewikkeld zijn om tot een afspraak te komen over de verdeling van inkomsten en uitgaven, alle partijen hebben daar belang bij.

Terug naar het schema, dit is voor ons de kern van het bepalen van rendement. Alle partijen, alle inkomsten en uitgaven per partij en over een langere termijn. Maar, moet je nu voor elk project zo’n heel schema invullen en van elke partij de inkomsten en uitgaven kennen? In het ideale geval natuurlijk wel, in de praktijk zal dat vaak lastig zijn. Maar het schema kan wel helpen in het structureren van de discussie. Het begint bij het inventariseren van de partijen en vervolgens met hun inkomsten en uitgaven. Dat laatste kan ook kwalitatief, met plusjes en minnetjes voor uitgaven en inkomsten en heel veel plusjes en minnetjes voor hele grote inkomsten en uitgaven. Zo krijg je in ieder geval een beeld hoe de inkomsten en uitgaven verdeeld zijn. Dat kan in eerste instantie gewoon achter een bureau met behulp van gezond verstand.

Conclusies

Met het schema hebben we ook een aantal factoren in beeld die belangrijk zijn bij het bepalen van het rendement. Zo zien we wat kunnen we doen als we een negatief rendement hebben:

Kijken of we werkelijk alle partijen in beeld hebben. Zijn we partijen vergeten die ook profiteren van deze ingreep, dan kunnen we die opnemen in dit schema. Maar, mogelijk zijn er ook partijen die kosten moeten maken vanwege onze ingreep, die moeten we dan ook meenemen.
We kunnen nog eens kritisch kijken naar alle inkomsten en uitgaven. Hebben we werkelijk alles in beeld? Kunnen we bezuinigen op de uitgaven en de inkomsten vergroten (efficiency)?
We kunnen nog eens kritisch kijken naar de gehanteerde termijn. Ons overzicht stopt bij vier jaar, wat gebeurt er in jaar vijf en zes? Als inkomsten en uitgaven niet dramatisch veranderen gloort er een aantrekkelijk rendement aan de horizon. Maar, met een langere termijn worden ook de onzekerheden groter, daarmee komen we op het vierde punt.
Aandacht voor de risico’s. Dit is natuurlijk niet alleen van belang bij een negatief rendement, juist als we denken een positief rendement te hebben is een duidelijk beeld van de risico’s noodzakelijk. Kijk nog eens kritisch naar alle aannames, reken een worst case scenario door en probeer argumenten te zoeken die tegen de ingreep pleiten. Kortom probeer tot een robuust voorstel te komen door kritisch naar het project te kijken.

De oplettende lezer zal opgemerkt hebben dat we geen rekening hebben gehouden met het tijdsaspect van geld. Om kort te zijn, € 100,= nu is meer dan € 100,= over vier jaar. Immers als je het nu op de bank heb je over vier jaar meer geld. Daarover meer in de volgende aflevering.

Rendement (1), eenvoudige casus

Rendement is een centraal begrip in onze beslisboom, eigenlijk een kantelpunt. Want zonder positief rendement heeft het volgens ons geen zin verder na te denken over de financiering. In een korte serie willen we het begrip rendement verder onderzoeken. In deze eerste aflevering beginnen we bij een verkenning van financieel rendement in een eenvoudige situatie. In een aantal afleveringen verdiepen we naar rendement in bredere zin en in complexere situaties (meerdere partijen) om af te sluiten met de discussie of het wel wenselijk is altijd in rendement te denken. Voor de lezers die financieel goed onderlegd zijn zullen de eerste artikelen mogelijk niet zoveel nieuws bieden maar die raken hopelijk uiteindelijk alsnog geprikkeld.

De aanleiding voor deze reeks is een aantal workshops dat we de afgelopen tijd gegeven hebben. We laten vaak een eenvoudig schema zien waarmee we rendement toelichten. Daar komen dan weer kritische vragen over. Logisch, als je het eenvoudig maakt moet je zaken weglaten en kritische luisteraars willen daar dan juist weer meer over weten. Reden voor ons om het verhaal over rendement verder uit te werken.

Eenvoudig geval

Laten we beginnen met een eenvoudig voorbeeld, een investering door één partij. Ik, eigenaar van een woning overweeg de aanschaf van een zonnepaneel. Denkend aan rendement kijk ik wat een paneel kost, wat de bijkomende kosten zijn voor bijvoorbeeld advies en installatie en wat het paneel jaarlijks oplevert (en eventueel kost aan onderhoud). Een simpel rekensommetje laat zien wat de terugverdientijd is en op basis daarvan kan ik voor mezelf bepalen of dit wel of geen goede investering is. Met andere woorden ik bepaal of ik het rendement voldoende vind.

Levert een investering in een zonnepaneel een goed rendement op dan ga ik verder met mijn project. Ik kan bijvoorbeeld een financieringsconstructie zoeken of het van mijn eigen spaarrekening betalen. Is er in mijn ogen niet voldoende rendement, dan heeft het geen zin om naar allerlei constructies als leasen of geld lenen te kijken. Daar wordt mijn project in principe alleen maar duurder van. Alleen iemand die mij geld geeft (een subsidie) kan de investering voor mij aantrekkelijk maken.

Bij een negatief of te laag rendement moet ik een stap terug in onze beslisboom en kijken hoe ik de ingreep efficiënter kan maken. Is er een ander paneel dat goedkoper is of meer opbrengt? Een andere installateur die goedkoper is? Kan ik een deel van het werk zelf doen? Met andere woorden mijn stapje terug is kijken of ik de uitgaven kan verlagen en de inkomsten kan verhogen. Dat is de manier om aan een beter rendement te werken. Hippe termen als verdienmogelijkheden en verdienmodellen komen uiteindelijk allemaal neer op het verhogen van de inkomsten en het verlagen van de uitgaven. Kom ik na allerlei aanpassingen alsnog uit op een positief rendement, dan ga ik onderzoeken hoe ik de financiering regel. Overigens moet ik daarbij natuurlijk niet vergeten dat het berekenen van mijn rendement een voorspelling voor de toekomst betreft. Ik moet daarom kritisch kijken naar allerlei aannames die ik maak, zoals de levensduur, de energieprijzen, de restwaarde etc.

Focus op doel

Maar, ik kan nog een stap verder terug in onze beslisboom. Een kritische kijk, wat was eigenlijk de aanleiding voor mijn project? Wat was het doel waarvoor ik een zonnepaneel aan wil schaffen? Een lagere energierekening? CO2 reductie? Een mooier dak? Als het rendement onvoldoende is, is het goed terug te gaan naar het doel en de vraag “waarom” te stellen. We komen snel in de verleiding om de oplossing centraal te stellen en de aanleiding, het probleem te vergeten. Lees nog eens ons artikel over Parkstad Limburg, een mooi voorbeeld waar het middel centraal staat. Als ik terug ga naar mijn doel kan ik ook allerlei alternatieve ingrepen agenderen. Stel het gaat mij om CO2 reductie, dan zou ik in plaats van investeren in zonnepanelen kunnen investeren in zuinige verlichting, mijn huis kunnen isoleren, een windmolen kopen (of investeren in een molen), de auto weg doen etc. Voor al deze ingrepen kan ik vervolgens het financiële rendement berekenen en zo het beste scenario kiezen. Overigens kan het ook zo zijn dat ik het gewoon leuk vind om zonnepanelen op mijn dak te hebben, dat is uiteraard ook een legitiem doel. Hoe we dat meenemen in ons rendement komt later aan de orde.

Wij merken in projecten dat er vaak te weinig nagedacht wordt over het doel of de aanleiding en de oplossing een eigen leven gaat leiden. De strategie is doorvragen over het waarom van een ingreep. Waarom willen we dit? Wat gebeurt er als je het niet doet? Gaat er dan wat mis? Wie heeft er dan een probleem? etc. Dit is al belangrijk bij mijn eenvoudige geval, maar wordt nog belangrijker bij complexe projecten. Er zijn meer partijen bij betrokken, de looptijd wordt langer, er is mogelijk al een soort informele consensus etc. Grote kans dat niemand meer duidelijk heeft waarom we hier ooit aan zijn begonnen. Daar komt bij dat er allerlei belangen kunnen spelen die het financiële rendement niet ten goede komen. Denk aan een adviseur die goede banden heeft met een leverancier of zelfs commissie krijgt.

Conclusies

Rendement verhogen is inkomsten vergroten, uitgaven verkleinen.
Als het rendement te laag is, heeft verder nadenken over de financiering geen zin
Rendement hangt samen met de aanleiding en het doel. Als we het doel uit het oog verliezen heeft het geen zin meer om over rendement te praten.

Residuele grondwaarde: wat is dat eigenlijk?

We merken het telkens weer: het begrip ‘residuele grondwaarde’, zoals dat in de wereld van bouwen en wonen veelvuldig wordt gebruikt, is lastig. Daarom een poging om het hier op zijn simpels uit te leggen. Twee dingen vooraf. Eén: ik sluit me aan bij het normale taalgebruik en heb het dus over waarde. In eerdere blogs ben ik al in gegaan op het verschil tussen ‘waarde’ en ‘prijs’. Twee: het begrip residuele grondwaarde speelt ook een belangrijke rol in onze infographic ‘wie verdient er aan bouwgrond?’ (te vinden onder het tabje ‘infographics’).

Een bonnetje

Stel ik geef u een bonnetje. Met dat bonnetje kun je ergens (bij de supermarkt, het postkantoor of de boekhandel) € 100 afhalen. Wat is dat bonnetje je waard? Hoeveel wil je ervoor geven? Ik stel deze vraag regelmatig in workshops. Het antwoord is meestal iets tussen de € 50 en € 75. Mensen vertrouwen het niet, krijg ik dat geld wel echt? En terwijl ik zeker weet dat ik mijn aankoopprijs kwijt ben, weet ik nog niet 100% zeker of ik die € 100 ook echt ga ontvangen. In principe luidt het antwoord: als ik zeker weet dat ik voor dat bonnetje inderdaad € 100 terug krijg dan is dat bonnetje me ook € 100 waard. In de praktijk iets minder omdat je toch liever meteen echt geld hebt en je moeite moet doen het bonnetje in te leveren. Het verschil tussen wat je er écht voor wilt betalen en die € 100 noemen we dan de ‘discount’ of korting.

Nog een bonnetje

Goed, nu hebben we weer zo’n zelfde bonnetje maar nu kun je er elk jaar en dat 5 jaar lang € 100 mee afhalen bij het postkantoor. Wat is het bonnetje je nu waard? Volgens dezelfde redenering als hiervoor: € 500 met een discount. En de discount is nu groter want voor die laatste € 100 moet je wel 5 jaar wachten. Je kunt je geld beter tussentijds op de bank zetten want dan krijg je een vergoeding (rente).

Als ik de redenering met het bonnetje nu veralgemeniseer: een bonnetje dat recht geeft op x maal jaarlijks y Euro is waard x keer y Euro met een discount die rekening houdt met renteverlies, risico en transactiekosten.

De waarde van een aandeel

Wat is volgens dezelfde redenering dan de waarde van een aandeel? Een aandeel geeft aan dat je eigenaar bent van een deel van een bedrijf. Dat bedrijf maakt als het goed is winst en soms wordt die winst uitgekeerd aan de aandeelhouders. Zo’n uitkering op een aandeel heet dividend. Het aandeel is in wezen een bonnetje dat je recht geeft op periodieke dividend uitkeringen.

Dus wat ben je bereid te betalen voor een aandeel dat je x maal jaarlijks y Euro dividend uit belooft te keren? Welnu: x maal y Euro met een discount die hier nog iets hoger is omdat een bedrijf failliet kan gaan (of slechter presteert dan beloofd). Maar hier speelt misschien nog wat anders. Een aandeel kun je makkelijk tussentijds verkopen. Als je daar rekening mee houdt dan wil je voor je aandeel betalen: x keer die y Euro aan dividend die ik denk te ontvangen + de verwachte opbrengst van dat aandeel als ik dat na die x jaren aan iemand anders ga verkopen.

Maar wat is die ‘iemand anders’ bereid dán voor jouw aandeel te betalen? Volgens dezelfde redenering: het aantal keren dividend wat die persoon denkt te ontvangen ná koop van dat aandeel. En weer de verwachte verkoopprijs van het aandeel aan weer de volgende koper.

Dit is misschien wat technisch of wiskundig maar je kunt aantonen dat die extra verkoopmogelijkheid in wezen neerkomt op een oneindige aaneenschakeling is van steeds weer nieuwe dividend uitkeringen. De waarde van een aandeel is, of je nu wel of niet tussentijds verkoopt, de optelling van alle dividenden zolang het bedrijf blijft bestaan rekening houdend met de discount. In technisch jargon: de waarde van een aandeel is de contant gemaakte stroom te verwachten dividenden.

De waarde van grond (1)

Zo kunnen we ook naar grond kijken. Wat ben je bereid te betalen voor een lapje grond? De grond is mij waard: het aantal keren opbrengst die die grond mij als eigenaar gaat opleveren. Rekening houdend met eventuele kosten die ik daarvoor moet maken.

Nemen we landbouwgrond. Die grond is waard het aantal oogsten aan graan (de opbrengst daarvan) rekening houdend met de arbeid die ik daarvoor moet verrichten. Als door wat voor reden dan ook de oogsten hoger uitvallen dan zal de grond dus meer waard worden. Hier is ook een van de uitspraken van oereconoom David Ricardo op gebaseerd: graan is niet duur omdat de grond duur is, maar grond is veel waard omdat graan veel opbrengt.

De waarde van grond (2)

Maar we weten dat de waarde van agrarische grond niet zo heel hoog is. Het wordt pas interessant als je huizen mag bouwen op die grond. Maar dat is vreemd: als de waarde van grond met huizen zo hoog is, waarom zou iemand er dan nog graan op gaan verbouwen? Simpel: omdat je niet overal huizen mag bouwen. We hebben het hier over een gereguleerde markt. En hier ligt ook de kern van het grondprijzen-beleid: een eenvoudige aanpassing van de wet (het bestemmingsplan) die toestaat dat een bepaald stukje grond verandert van agrarische bestemming naar woonbestemming zal van de ene op de andere dag vele malen in waarde stijgen.

Maar wat is de waarde van grond als je er een huis op mag bouwen? We nemen weer dezelfde basisredenering. Ik wil voor die grond betalen: de verwachte verkoopprijs van dat huis dat ik ga bouwen minus de kosten die ik moet maken om dat huis te kunnen bouwen op die grond. Let op: het gaat dus om een verwachting die je nu maakt over de toekomst. Je weet immers niet zeker wat je voor dat huis gaat krijgen als het daadwerkelijk af is.

En eindelijk hebben we het begrip ‘residuele grondwaarde’ te pakken. Het is de prijs die je maximaal wilt betalen (het punt waarop je net geen winst meer maakt) voor de grond rekening houdend met de te verwachten verkoopprijs van de woning in de toekomst minus de kosten voor het bouwen van dat huis (de zogenaamde stichtingskosten, de stenen, het cement, de werklui en zo verder).

De waarde van een woning

Blijven we nog zitten met de waarde van een woning. Hoe weten we wat een woning waard is? Die waarde hangt om te beginnen van allerlei externe factoren af. De stand van de economie (crisis of voorspoed), demografische factoren, de unieke ligging van het huis etc. Maar ook van allerlei fiscale factoren zoals de aftrekbaarheid van rente-kosten op de hypotheek (lening die je maakt om het huis te kunnen kopen).

Maar toch kunnen we weer dezelfde basis redenering van stal halen om de waarde van een huis te bepalen. Economen doen daar heel makkelijk over: we zien af van allerlei fiscale verstoringen en we doen alsof er maar één type huis is. Wat een huis in wezen doet is jou ‘woondiensten’ bieden. Een woondienst mag je vergelijken met ‘grondopbrengsten’, ‘dividend’ uit de eerdere voorbeelden. Een huis biedt jou dus een hele reeks jaarlijkse woondiensten.

Wat wil je betalen voor die reeks woondiensten? Daarvoor kijk je naar de alternatieven. We hadden al de flauwe vooronderstelling gemaakt dat er geen belastingtrucs zijn en dat alle huizen identiek zijn (qua uiterlijk en ligging). Je kunt dus kiezen: een huis huren of een huis kopen. Als je een huis gaat huren dan is het simpel. Je bent dan kwijt: de som aan huurpenningen die je moet betalen voor je woondiensten over een hele reeks jaren. Een econoom zegt dan: je wilt voor je huis dan niet meer betalen dan diezelfde stroom aan huurpenningen die je bij huur kwijt zou zijn (rekening houdend met rente-verlies etc). De waarde van een huis is in dit simpele voorbeeld dus gelijk aan de stroom huurpenningen die je bespaart door het huis te kopen.

Residuele grondwaarde: Ricardo revisited

Nu terug naar de (residuele) grondwaarde. Stel nu dat er ineens krapte op de woningmarkt komt. Er komen meer jongeren op de markt of de economie zit in een hausse of iemand bedenkt een fiscale tegemoet koming etc. Huizen zullen dan zomaar meer waard gaan worden (ervan uitgaand dat er niet ook meteen meer huizen gebouwd kunnen of mogen worden).

Ricardo zei: als graan meer gaat opleveren dan gaat de prijs van grond omhoog. De speculanten zeggen in navolging van Ricardo: als de prijs van woningen omhoog gaat, dan wordt de waarde van mijn stukje grond hoger. De truc is dus om zo vroeg mogelijk agrarische grond op te kopen tegen lage prijzen en te speculeren op een verandering in bestemming of op toekomstige stijging van huizenprijzen.

Daar is jarenlang heel veel geld mee verdiend. Door speculanten, door projectontwikkelaars, maar ook door gemeenten en huizenbezitters. De keerzijde is natuurlijk dat naarmate je later instapt op deze trein je meer risico gaat lopen en hogere verliezen kunt realiseren. En dat is wat we de laatste 5 jaar of zo om ons heen zien gebeuren.

Rudy van Stratum

Eerder maakten we een infographic over het ontstaan van grondwaarde (zie voor ontstaan van deze infographic ook deze pagina).

Eén procent rente voor de schildpad?

Bas Haring bespreekt vandaag in de VK een interessante economische vraag: waarom is de rente altijd ergens zo tussen de 1 en de 10 procent? En zelden tot nooit negatief of 100%?

De redenering

Laten we de redenering van Haring eens volgen. Dat er rente wordt gevraagd vindt Haring wel logisch. Immers: als ik mijn auto aan iemand anders uitleen, dan wil ik hem een keer terug krijgen. Dus geld wil je ook terug krijgen als je dat aan iemand anders uitleent. En bij die auto: ik wil niet alleen de auto terug maar ook een vergoeding voor ‘verlies’ of compensatie voor iets wat ik heb gemist door het uitlenen. Ik heb bijvoorbeeld met de trein moeten reizen en dat was duurder of onplezieriger en dus wil ik dat vergoed hebben.

Mijn reflectie. Mee eens. Rente is een vergoeding voor gederfde inkomsten en mogelijk risico van wanbetalen. Stel dat gedurende een jaar x% van alle leningen niet terug zou worden betaald dan zou je met alle uitleners bij elkaar een verzekering kunnen opzetten. Uit de pot zou dan compensatie voor wanbetalingen kunnen worden betaald. De premie die iedereen zou moeten betalen zou dan ongeveer x% (+ een beetje voor de administratie) moeten zijn. Zie hier de eerste verklaring van de hoogte van de rente: ongeveer de kans op wanbetaling.

Verder is er sprake van een zogenaamde tijdsvoorkeur. Wat dat precies is, is ook onder economen niet helemaal duidelijk. Voor een econoom is het een ‘datum’, een gegeven. Het heeft iets met de psychologie te maken en in onze serie denkfouten hebben we er een item aan gewijd. Het heeft te maken met onze beperkte levensduur, met hoe we evolutionair hebben overleefd en wat niet al. Waar het op neerkomt is dat we een sterke neiging hebben voor consumptie en genot in het heden (‘je kunt het maar gehad hebben’) en dus zul je (bovenmatig blijkt uit onderzoek) verleid moeten worden afstand te doen voor je consumptie nu in ruil voor (iets meer) consumptie later.

Overigens, iets wat zelden wordt genoemd (zie mijn bespreking van het boek van Greco elders op deze site): rente kan wel degelijk negatief zijn. Als banken elk moment failliet kunnen gaan en je dus gedwongen wordt het ‘baar’ in huis te houden dan ben je bereid te betalen voor het veilig in een kluis opbergen van je geld. Je betaalt dan ‘stallingskosten’ om diefstal of inbraak te voorkomen en jezelf een veilig gevoel te geven.

Rente kan ook extreem hoog zijn (100% of meer) als er sprake is van een bijzonder nijpende situatie. Het is dan een situatie van vraag en aanbod (dat is het overigens bijna altijd): als ik heel erg smacht naar het bezitten van een uniek product dat nu eenmalig langs komt en ik heb geen geld maar ik weet dat ik over een maand dat geld wel heb of krijg, dan ben ik bereid nu een dure lening aan te gaan om in het nu alsnog dat unieke product te bemachtigen.

Maar waarom 5%?

Maar inderdaad: de rente is bijna nooit negatief of meer dan 100%. Altijd ergens tussen de 1 en de 10% inderdaad. De redenering van Haring is dat dat te maken heeft met onze levensduur. Wat zou ik willen betalen voor een bosje met hout? Welnu, voor mijn 30e kan ik een bosje niet betalen en na mijn 60e heb ik geen zin meer om te hakken. Dus ik kan 30 jaar van een bosje profiteren en heb dus 30 jaar een houtkap-oogst. Dus ik wil betalen maximaal 30 keer de houtoogst. En op jaarbasis betekent dat 1/30 van het totaal en dat is 3,3 procent en dat is ongeveer 5%.

Het is volgens mij een kringredenering maar ik ben het op hoofdlijnen wel met Haring eens. Hoe zou een econoom het benaderen? Wat is een object je waard (in financiële zin)? De oogst is het dividend waar je als eigenaar recht op hebt. Het object is dan waard: de voor de tijd gecorrigeerde stroom dividenden of oogsten. Het rendement of de rente is dan het dividend gedeeld door de waarde van het object. Zie je dat het een kringredenering is? De truc zit hem in het zinnetje: voor de tijd gecorrigeerd. Wat je daar invult of aanneemt is meteen je rendement of je rente. Het is niet de uitkomst van de som maar de aanname vooraf.

Eindige levensduur?

Een eindige levensduur maakt in essentie niet zoveel uit. Je kunt tegen het einde van je leven het bosje weer doorverkopen. De prijs van het bosje zal alsdan weer zijn: het aantal oogsten wat het bosje nog op zal leveren voor de koper van dat moment (gecorrigeerd voor de tijd). Wat van belang is: de oogstcapaciteit van het bosje. Vaak is de aanname in rekensommetjes dat een object een eeuwigdurende constante vrucht of oogst aflevert. Oftewel: de oogst zal telkenjare tot in het oneindige een gelijke houtkap zijn.

In dat geval kun je aantonen dat de waarde van het bos gelijk is aan de oogst gedeeld door de rentevoet. Dus als de oogst 100 Euro is per jaar en de rentevoet (tijdsvoorkeur + risico) gelijk aan 5% dan is de waarde van het bos gelijk aan 100 / 0.05 oftewel € 2.000. Hier is dus sprake van een vermenigvuldig factor van 20 en die is dus gelijk aan 1 gedeeld door de rentevoet. Deze waarde is gelijk en vast zowel voor iemand die 50 jaar leeft als voor iemand die 500 jaar leeft. Je kunt immers op elk gewenst moment het bosje weer doorverkopen aan de volgende generatie. Dit is hoe een aandeel werkt bij een bedrijf dat elk jaar dividend uitkeert. Het bedrijf blijft eeuwigdurend bestaan en de aandeelhouder heeft een eindige levensduur.

Dus waarom is de rente dan 5%? Eerlijk gezegd weet ik het antwoord daarmee nog steeds niet. Het is duidelijk dat zonder tijdsvoorkeur, zonder inflatie en zonder enig risico de rente 0% zou kunnen of moeten zijn. Maar dat is niet het geval in de praktijk. Een deel van die 5% is te herleiden tot onzekerheid over het vroegtijdig overlijden van bedrijven of bossen (en niet van personen dus). En het resterende deel van die 5% is te herleiden tot de goeddeels onbegrepen component van de tijdsvoorkeur. En dat laatste zou wel eens heel goed met de perceptie van een eindige leeftijd van de actor/persoon te maken kunnen hebben!

Rudy van Stratum